binary-search

#review

概述

二分搜索算法的原理和猜数字游戏类似，就是那个有人说 " 我正想着一个 1 到 100 的数字 " 的游戏。我们每回应一个数字，那个人就会说这个数字是高了、低了还是对了。

这个算法要求被搜索的数据结构已排序，以下是该算法遵循的步骤：

选择数组的中间值
如果选中值是待搜索值，算法执行完毕（值找到了）
如果待搜索值比选中值要小，则返回步骤 1 并在选中值左边的子数组中寻找
如果待搜索值比选中值要大，则返回步骤 1 并在选种值右边的子数组中寻找

特点

排序的数组
查找的次数少
要查找的目标具有单调性

二分查找

35. 搜索插入位置

题目

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

输入: [1,3,5,6], 5
输出: 2

输入: nums = [1,3,5,6], target = 2
输出: 1

输入: nums = [1,3,5,6], target = 7
输出: 4

分析

分析：根据题意并结合题目给出的 4 个示例，不难分析出这个问题的等价表述如下：

如果目标值（严格）大于排序数组的最后一个数，返回这个排序数组的长度，否则进入第 2 点。
返回排序数组从左到右，大于或者等于目标值的第 1 个数的索引。

事实上，当给出数组中有很多数和目标值相等的时候，我们返回任意一个与之相等的数的索引值都可以，不过为了简单起见，也为了方便后面的说明，我们返回第 1 个符合题意的数的索引。

题目告诉你“排序数组”，其实就是在疯狂暗示你用二分查找法。二分查找法的思想并不难，但写好一个二分法并不简单，下面就借着这道题为大家做一个总结。

注意

一定得返回左边界 left，

如果返回右边界 right 提交代码不会通过

理由是对于 [1,3,5,6]，target = 2，返回大于等于 target 的第 1 个数的索引，此时应该返回 1

在上面的 while (left <= right) 退出循环以后，right < left，right = 0 ，left = 1

根据题意应该返回 left，

如果题目要求你返回小于等于 target 的所有数里最大的那个索引值，应该返回 right

选择一个最简单的例子，决定返回 left 还是 right 即可

传统二分查找法模板

刚接触二分查找法的时候，使用上面的模板，我们可能会像下面这样写代码，我把这种写法容易出错的地方写在了注释里：

说明

当你把二分查找法的循环可以进行的条件写成 while (left <= right) 的话，在写最后一句 return 的时候，如果你不假思索，把左边界 left 返回回去，你写对了，但为什么不返回右边界 right 呢？

但是事实上，返回 left 是有一定道理的，如果题目换一种问法，你可能就要返回右边界 right，这句话不太理解没有关系，我也不打算讲得很清楚（在上面代码的注释中我已经解释了原因），因为实在太绕了，这不是我要说的重点。

可见：传统二分查找法模板，当退出 while 循环的时候，在返回左边界还是右边界这个问题上，比较容易出错。

那么，是不是可以回避这个问题呢？答案是肯定的，答案就在下面我要介绍的“神奇的”二分查找法模板里。

“神奇的”二分查找法模板

二分查找法的思想：二分查找法的思想是“夹逼”，或者说“排除”，而“二分”只是手段，即“通过二分排除了候选区间的一大半的非目标元素”

具体说来，如下：在每一轮循环中，都可以排除候选区间里将近一半的元素，进而使得候选区间越来越小，直至有限个数（通常为 1 个），而这个数就有可能是我们要找的数（在一些情况下，还需要单独做判断）。

在一些资料中，你可能看过别人写二分查找法，把循环可以进行的条件写成 while (left < right) ，当时你是不是跟我一样有疑问：“咦？当左右边界一样的时候，那个数岂不是会被漏掉”。但是我要告诉你，这样写在绝大多数情况下是最好的，这也是“神奇的”二分查找法模板好用的一部分。

理由很简单：写 while (left < right) 的时候，退出循环时，左边界等于右边界，因此你不必纠结要返回 left 还是 right ，此时返回 left 或者 right 都是可以的。

回到这一节最开始的疑问：“区间左右边界相等（即收缩成 1 个数）时，这个数是否会漏掉”，解释如下：

如果你的业务逻辑保证了你要找的数一定在左边界和右边界所表示的区间里出现，那么可以放心地返回 l 或者 r，而无需再做判断；即使这个数 nums[left]&&nums[right] 没有经过 while 循环内的判断，很多时候这个数就是正确的答案
如果你的业务逻辑不能保证你要找的数一定在左边界和右边界所表示的区间里出现，那么只要在退出循环以后，再针对 nums[left] 或者 nums[right] （此时 nums[left] == nums[right]）单独作一次判断，看它是不是你要找的数即可，这一步操作常常叫做“后处理”。

var searchInsert = function (nums, target) {
    let len = nums.length;

    if (len == 0) {
        return 0;
    }
    if (target > nums[-1]) return size

    let left = 0
    let right = len - 1

    while (left < right) {
        let mid = (left + right) >>> 1
        if (nums[mid] < target) {
            left = mid + 1
        } else {
            right = mid
        }
    }
	// 后处理
    return nums[left] < target ? left + 1 : left;
}

模板总结

确定范围区间，一般就是 [0,len-1]，思考边界特例
循环条件 left<right
默认取左中位数 mid = (left+right)>>>1

分支逻辑先写可以排除中位数的逻辑，另一个分支无需排除中位数

if (nums[mid] < target) {
  // 中位数肯定不对, 需要排除中位数, 通过 left 排除
  left = mid + 1
} else {
  right = mid 
}

确认中位数的选择

排除中位数的逻辑是 left，选择左中位数，可以被排除，不会进入死循环
排除中位数的逻辑是 right，选择右中位数，可以被排除，不会进入死循环

退出循环，视情况判断 left&&right 是否符合题意
返回 left&&right

69. X 的平方根

153. 寻找旋转排序数组中的最小值

简单实现

一遍遍历，直接使用内置的 Math.min() 函数

利用旋转序列的特性，一直升序，在改变的一刻，即是最小值

  class Solution {
  public:
      int findMin(vector<int>& nums) {
          int i=0,n=nums.size()-1;
          while(i<n){
              if(nums[i+1]>=nums[i])
                  i++;
              else
                  return nums[i+1];
          }
          return nums[0];
      }
  };

时间复杂度都是 O(n)

分析

旋转过后的数组存在一个最小值 x：

所有在 x 左侧元素 > 数组第一个元素
所有在 x 右侧元素 < 数组第一个元素

如果旋转点在数组的两端，数组依然是有序的

找到数组的中间元素 mid：
如果中间元素 > 数组第一个元素，我们需要在 mid 右边搜索变化点。
如果中间元素 < 数组第一个元素，我们需要在 mid 左边搜索变化点。

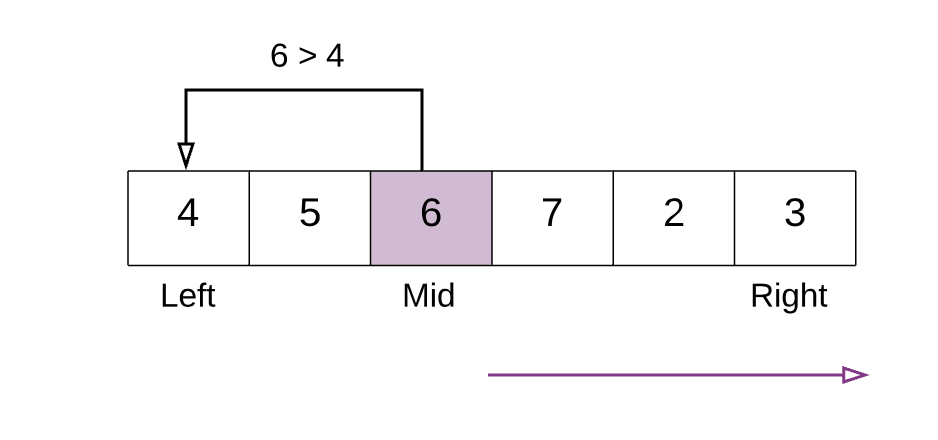
上面的例子中，中间元素 6 比第一个元素 4 大，因此在中间点右侧继续搜索。

当我们找到变化点时停止搜索，当以下条件满足任意一个即可：
- nums[mid] > nums[mid + 1]，此时 mid+1 是最小值。
- nums[mid - 1] > nums[mid] 此时 mid 是最小值。

实现

  /**
   * @param {number[]} nums
   * @return {number}
   */
  var findMin = function(nums) {
    const len = nums.length
    if(len===0) return nums[0]
    let left = 0,right = len -1
    if (nums[right] > nums[0]) {
      return nums[0];
    }
    while(left<=right){
      const mid = (left+right)>>>1
      if(nums[mid] > nums[mid + 1]) return nums[mid+1]
      if(nums[mid - 1] > nums[mid]) return nums[mid]
      if(nums[mid]>nums[0]) left = mid + 1
      if(nums[mid]<nums[0]) right = mid - 1
    }
    return -1
  };
  
  let nums = [3, 4, 5, 1, 2]
  console.log(findMin(nums))

模板实现

  var findMin = function (nums) {
    const len = nums.length
    if (len <= 1) return nums[0]
    let left = 0, right = len - 1
    // 旋转没有影响顺序
    if (nums[right] > nums[0]) {
      return nums[0];
    }
    while (left < right) {
      const mid = (left + right) >>> 1
      if (nums[mid] > nums[right]){
        left = mid + 1
      }else{
        right = mid
      }
    }
    return nums[left]
  };

这题的难点在于找准排除中位数的逻辑，和 nums[0],nums[len-1],nums[left],nums[right] 哪一个作比较才可以保证排除中位数

154. 寻找旋转排序数组中的最小值 II

区别

注意数组中可能存在重复的元素。

  let nums = [2,2,2,0,1]
  输出: 0

模板实现

var findMin = function (nums) {
    const len = nums.length
    if (len === 1) return nums[0]
    let left = 0, right = len - 1
    while (left < right) {
        const mid = (left + right) >>> 1
        if (nums[mid] > nums[right]) {
            left = mid + 1
        } else if (nums[mid] < nums[right]) {
            right = mid
        } else {
            // [3,3,3,1,3,3]
            right = right - 1
        }
    }
    return nums[left]
};

33. 搜索旋转排序数组

模板实现

实现不了, 边界条件太多了

常规的二分法也很难思考到细节, 还是降维的方法更好

287. 寻找重复数

1095. 山脉数组中查找目标值

题目

给你一个 山脉数组 mountainArr，请你返回能够使得 mountainArr.get(index) 等于 target ，且使得其下标 index 值最小
如果不存在这样的下标 index，就请返回 -1。
你将不能直接访问该山脉数组，必须通过 MountainArray 接口来获取数据：
- MountainArray.get(k) - 会返回数组中索引为 k 的元素（下标从 0 开始）
- MountainArray.length() - 会返回该数组的长度

分析

理解“山脉数组”，“山脉数组”可以根据山顶分为两部分，“前有序数组”是升序数组，“后有序数组”是降序数组
题目还告诉我们“对 MountainArray.get 发起超过 100 次调用的提交将被视为错误答案”，就在疯狂暗示你使用时间复杂度低的算法，对于有序数组当然使用“二分查找法”。
第 1 步：先找到山顶元素 mountaintop 所在的索引。
第 2 步：在前有序且升序数组中找 target 所在的索引，如果找到了，就返回，如果没有找到，就执行第 3 步；
第 3 步：如果步骤 2 找不到，就在后有序且降序数组中找 target 所在的索引。

实现

/**
 * // This is the MountainArray's API interface.
 * // You should not implement it, or speculate about its implementation
 * function MountainArray() {
 *
 *     @param {integer} index
 *     @return {integer}
 *     this.get = function(index) {
 *         ...
 *     };
 *
 *     @return {integer}
 *     this.length = function() {
 *         ...
 *     };
 * };
 */
/**
 * @param {number} target
 * @param {MountainArray} mountainArr
 * @return {number}
 */
var findInMountainArray = function (target, mountainArr) {
  const len = mountainArr.length()
  // 步骤 1：先找到山顶元素所在的索引
  const peakIndex = findInMountainArrayPeak(mountainArr, 0, len - 1)
  // 步骤 2：在前有序且升序数组中找 target 所在的索引
  const targetLeft = findIncrease(target,mountainArr,0,peakIndex)
  if(targetLeft!==-1) return targetLeft
  // 步骤 3：如果步骤 2 找不到，就在后有序且降序数组中找 target 所在的索引
  const targetRight = findDecrease(target,mountainArr,peakIndex+1,len-1)

  return targetRight
    
  function findInMountainArrayPeak(mountainArr, left, right) {
    while (left < right) {
      const mid = (left + right) >>> 1
      if (mountainArr.get(mid) < mountainArr.get(mid + 1)) {
        // 如果当前的数比右边的数小，它一定不是山顶
        left = mid + 1;
      } else {
        right = mid;
      }
    }
    return left
  }
  function findIncrease(target,mountainArr,left,right){
    while(left<right){
      const mid = (left+right)>>>1
      if(mountainArr.get(mid) < target){
        left = mid+1
      }else{
        right = mid
      }
    }
    return mountainArr.get(left)===target?left:-1
  }
  function findDecrease(target,mountainArr,left,right){
    while(left<right){
      const mid = (left+right)>>>1
      if(mountainArr.get(mid) > target){
        left = mid+1
      }else{
        right = mid
      }
    }
    return mountainArr.get(left)===target?left:-1
  }
}

658. 找到 K 个最接近的元素

题目

给定一个排序好的数组，两个整数 k 和 x，从数组中找到最靠近 x（两数之差最小）的 k 个数。返回的结果必须要是按升序排好的。如果有两个数与 x 的差值一样，优先选择数值较小的那个数。
```
let nums = [1,2,3,4,5], k=4, x=3
输出: [1,2,3,4]
```

分析

一个一个删，因为是有序数组，且返回的是连续升序子数组，所以每一次删除的元素一定是位于边界；
一共 5 个元素，要保留 4 个元素，因此要删除 1 个元素；
因为要删除的元素都位于边界，于是可以使用双指针对撞的方式确定保留区间，即“最优区间”。
因为差值一样的时候优先选择较小的，所以优先删除右边界

实现

var findClosestElements = function(arr, k, x) {
  const len = arr.length
  let left = 0 , right = len - 1
  while(right-left>k-1){
    const diffL = x - arr[left]
    const diffR = arr[right] - x
    if(diffR>=diffL){
      right -=1
    }else{
      left +=1
    }
  }
  return arr.slice(left,right+1)
};

复杂度分析

时间复杂度：O(N)，这里 N 是数组的长度。
空间复杂度：O(1)，只使用了常数个额外的辅助空间。

二分法分析

题目中说有序数组，又易知：

1、题目要求返回的是区间，并且是连续区间；

2、区间长度是固定的，并且 k 的值为正数，且总是小于给定排序数组的长度，即 k 的值“不违规”；
因此，只要我们找到了左边界的索引，从左边界开始数 k 个数，返回就好了。我们把这件事情定义为“寻找最优区间”，“寻找最优区间”等价于“寻找最优区间的左边界”。因此本题使用二分查找法在有序数组中定位含有 k 个元素的连续子区间的左边界，即使用二分法找“最优区间的左边界”。

二分法实现

  var findClosestElements = function(arr, k, x) {
    const len = arr.length
    let left = 0 , right = len - k
    while(left<right){
      const mid = (right+left)>>>1
      if(x-arr[mid]>arr[mid+k]-x){
        left = mid+1
      }else{
        right = mid
      }
    }
    return arr.slice(left,left+k)
  };