common-algorithm

JS bench：https://jsbench.me/

复杂度

复杂度分析

复杂度也叫渐进复杂度，包括时间复杂度和空间复杂度，一个表示执行的快慢，一个表示内存的消耗，用来分析算法执行效率与数据规模之间的增长关系，可以粗略的表示，越高阶复杂度的算法，执行效率越低。

为什么需要复杂度分析

学习数据和算法就是为了解“快”和“省”的问题，也就是如何设计你的代码才能使运算效率更快，占用空间更小。那如何来计算代码执行效率呢？这里就会用到复杂度分析。

虽然我们可以用代码准确的计算出执行时间，但是这也会有很多局限性。

数据规模的不同会直接影响到测试结果。比如说同一个排序算法，排序顺序不一样，那么最后的计算效率的结果也会不一样；如果恰好已经是排序好的了数组，那么执行时间就会更短。又比如说如果数据规模比较小的话，测试结果可能也无法反应算法的性能。

测试的环境不同也会影响到测试结果。比如说同一套代码分别在 i3 和 i7 处理器上进行测试，那么 i7 上的测试时间肯定会比 i3 上的短。

所以需要一个不用准确的测试结果来衡量，就可以粗略地估计代码执行时间的方法。这就是复杂度分析。

大 O 复杂度表示法

以一个例子开始，请估算下面代码的执行时间

function total(n) { // 1
  var sum = 0; // 2
  for (var i = 0; i < n; i++) { // 3
    sum += i; // 4
  } //5 
} //6

我们假设每行代码执行的时间都一样，记做 t，那么上面的函数中的第 2 行需要 1 个 t 的时间，第 3 行和第 4 行分别需要 n 个 t 的时间，那么这段代码总的执行时间为 (2n+1)*t。

那么按照上面的分析方法，请估算下面代码的执行时间

function total(n) { // 1
  var sum = 0; // 2
  for (var i = 0; i < n; i++) { // 3 
    for (var j = 0; j < n; j++) { // 4
      sum = sum + i + j; // 5
    }
  }
}

第 2 行需要一个 t 的时间，第 3 行需要 n 个 t 的时间，第 4 行和第 5 行分别需要 n^2 个的时间，那么这段代码总的执行时间为 (2n^2+n+1)*t 的时间。

从数学角度来看，我们可以得出个规律：代码的总执行时间 T(n) 与每行代码的执行次数成正比：T(n) = O(f(n))

在这个公式中，T(n) 表示代码的执行时间；n 表示数据规模的大小；f(n) 表示每行代码执行的次数总和；O 表示代码的执行时间 T(n) 与 f(n) 表达式成正比。

所以上边两个函数的执行时间可以标记为 T(n) = O(2n+1) 和 T(n) = O(2n^2+n+1)。这就是大 O 时间复杂度表示法，它不代表代码真正的执行时间，而是表示代码随数据规模增长的变化趋势，简称时间复杂度。

而且当 n 很大时，我们可以忽略常数项，只保留一个最大量级即可。所以上边的代码执行时间可以简单标记为 T(n) = O(n) 和 T(n) = O(n^2)。

时间复杂度分析

那如何分析一段代码的时间复杂度呢，可以利用下面的几个方法

加法法则：

总复杂度等于量级最大的那段代码的复杂度。

function total(n) { 
  // 第一个 for 循环
  var sum1 = 0; 
  for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++) {
      sum1 = sum1 + i + j; 
    }
  }
  // 第二个 for 循环
  var sum2 = 0;
  for(var i=0;i<1000;i++) {
    sum2 = sum2 + i;
  }
  // 第三个 for 循环
  var sum3 = 0;
  for (var i = 0; i < n; i++) {
    sum3 = sum3 + i;
  }
}

我们先分别分析每段 for 循环的时间复杂度，再取他们中最大的量级来作为整段代码的时间复杂度。

第一段 for 循环的时间复杂度为 O(n^2)。

第二段 for 循环执行了 1000 次，是个常数量级，尽管对代码的执行时间会有影响，但是当 n 无限大的时候，就可以忽略。因为它本身对增长趋势没有影响，所以这段代码的时间复杂度可以忽略。

第三段 for 循环的时间复杂度为 O(n)。

总上，取最大量级，所以整段代码的时间复杂度为 O(n^2)。@

乘法法则

嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。

function f(i) {
  var sum = 0;
  for (var j = 0; j < i; j++) {
    sum += i;
  }
  return sum;
}
function total(n) {
  var res = 0;
  for (var i = 0; i < n; i++) {
    res = res + f(i); // 调用 f 函数
  }
}

单独看 total 函数的时间复杂度就是为 T1(n)=O(n)，但是考虑到 f 函数的时间复杂度也为 T2(n)=O(n)。所以整段代码的时间复杂度为 T(n) = T1(n) * T2(n) = O(n*n)=O(n^2)。

常见的时间复杂度分析

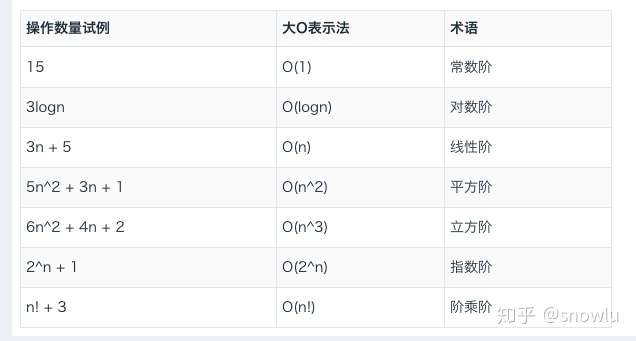
如上图可以粗略的分为两类，多项式量级和非多项式量级。其中，非多项式量级只有两个：O(2^n) 和 O(n!) 对应的增长率如下图所示

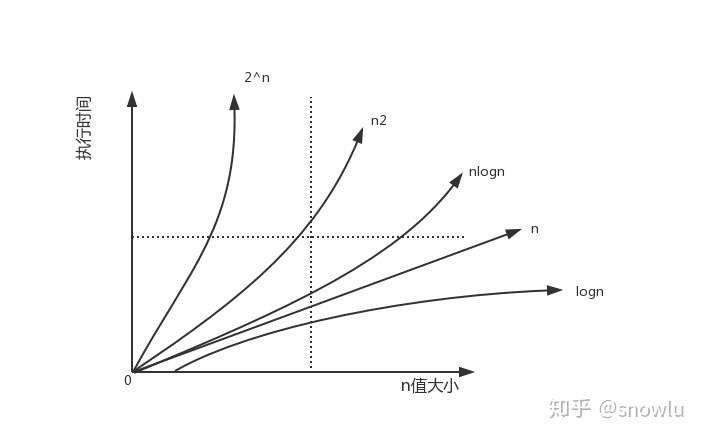
当数据规模 n 增长时，非多项式量级的执行时间就会急剧增加，所以，非多项式量级的代码算法是非常低效的算法。

O(1)

O(1) 只是常量级时间复杂度表示法，并不是代码只有一行，比如说下面这段代码

function total() {
  var sum = 0;
  for(var i=0;i<100;i++) {
    sum += i;
  }
}

虽然有这么多行，即使 for 循环执行了 100 次，但是代码的执行时间不随 n 的增大而增长，所以这样的代码复杂度就为 O(1)。

O(logn)、O(nlogn)@

对数阶时间复杂度的常见代码如下

function total1(n) {
  var sum = 0;
  var i = 1;
  while (i <= n) {
    sum += i;
    i = i * 2;
  }
}
function total2(n) {
  var sum = 0;
  for (var i = 1; i <= n; i = i * 2) {
    sum += i;
  }
}

上面两个函数都有一个相同点，变量 i 从 1 开始取值，每循环一次乘以 2，当大于 n 时，循环结束。实际上，i 的取值就是一个等比数列，就像下面这样

2^0 2^1 2^2 ... 2^k... 2^x =n;

所以只要知道 x 的值，就可以知道这两个函数的执行次数了。那由 2^x = n 可以得出 x = log2^n，所以这两个函数的时间复杂度为 O(log2^n)。

再看下面两个函数的时间复杂度

function total1(n) {
  var sum = 0;
  var i = 1;
  while (i <= n) {
    sum += i;
    i = i * 3;
  }
}
function total2(n) {
  var sum = 0;
  for (var i = 1; i <= n; i = i * 3) {
    sum += i;
  }
}

由上可以得知，这两个函数的时间复杂度为 O(log3^n) 。

由于我们可以忽略常数，也可以忽略对数中的底数，所以在对数阶复杂度中，统一表示为 O(logn)；那 O(nlogn) 的含义就很明确了，时间复杂度为 O(logn) 的代码执行了 n 次。

O(m+n)、O(m*n)@

function total(m,n) {
  var sum1 = 0;
  for (var i = 0; i < n; i++) {
    sum1 += i;
  }
  var sum2 = 0;
  for (var i = 0; i < m; i++) {
    sum2 += i;
  }
  return sum1 + sum2;
}

因为我们无法评估 m 和 n 谁的量级比较大，所以就不能忽略掉其中一个，这个函数的复杂度是有两个数据的量级来决定的，所以此函数的时间复杂度为 O(m+n)；那么 O(m*n) 的时间复杂度类似。

空间复杂度分析

空间复杂度的话和时间复杂度类似推算即可。所谓空间复杂度就是表示算法的存储空间和数据规模之间的关系。

比如说分析下面代码的空间复杂度：

function initArr(n) {
  var arr = [];
  for (var i = 0; i < n; i++) {
    arr[i] = i;
  }
}

根据时间复杂度的推算，忽略掉常数量级，每次数组赋值都会申请一个空间存储变量，所以此函数的空间复杂度为 O(n)。

常见的空间复杂度只有 O(1)、O(n)、O(n^2)。其他的话很少会用到。

复杂度优化

function total(n) {
  var sum = 0;
  for (var i = 1; i <= n; i++) {
    sum += i;
  }
  return sum;
}

此函数的时间复杂度你现在应该很容易就能看出来了，为 O(n)。

我觉得这个时间复杂度有点高了，我想要 O(1) 的时间复杂度函数来实现这个算法，可以吗？

可以的，小数学神童高斯教会我们一招，如下

function total(n) {
  var sum = n*(n+1)/2
  return sum;
}

此函数的时间复杂度仅仅为 O(1)，在数据规模比较庞大的时候，下面的函数是不是明显比上面的函数运算效率更高呢。

最好、最坏时间复杂度分析

function find(n, x, arr) {
  let ind = -1;
  for (let i = 0; i < n; i++) {
    if (arr[i] === x) ind = i;
  }
  return ind;
}

上面函数的功能就是查找一个变量 x 是否在数组 arr 中，如果在的话，返回所在的位置，否则就返回 -1。通过上一节的学习分析，这个函数的时间复杂度就很容易知道了，为 O(n)。

接下来，稍微优化下这个 find 函数，如果查找到目标的话，就没必要再往后查找了。

function find(n, x, arr) {
  let ind = -1;
  for (let i = 0; i < n; i++) {
    if (arr[i] === x){
      ind = i;
      break;
    } 
  }
  return ind;
}

现在代码的时间复杂度还为 O(n) 吗？不确定，利用上一章的分析法就无法解决了。

因为要查找的变量 x 可能会出现在数组的任意位置。如果变量 x 恰好是数组中第一个元素，那么函数就会 break ，后续就不会继续遍历了，那时间复杂度就是 O(1)。但如果恰好是数组中第末个元素，或者数组中不存在变量 x 的话，那就需要把整个数组都遍历一遍，时间复杂度就成了 O(n)。所以，不同的情况下，这个函数的时间复杂度是不一样的。

为了表示代码在不同情况下的不同时间复杂度，需要了解以下三个概念：最好情况时间复杂度、最坏情况时间复杂度和平均情况时间复杂度

理想情况

最好情况时间复杂度：在最理想的情况下，执行这段代码的时间复杂度。比如说刚才那段函数，在最理想的情况下，要查找的变量 x 正好是数组的第一个元素，这种情况下对应的时间复杂度就是最好情况时间复杂度。

糟糕情况

最坏情况时间复杂度：在最糟糕的情况下，执行这段代码的时间复杂度。比如说刚才那段函数，要查找的变量 x 正好是数组的第末个元素或者不在数组中存在，查找函数就会把数组都遍历一遍，这种情况下对应的时间复杂度就是最坏情况时间复杂度。

平均情况

但是，最好情况时间复杂度和最坏情况时间复杂度对应的都是极端情况下的代码复杂度，发生的概率其实并不大。

为了更好地表示平均情况下的复杂度，引入另一个概念：平均情况时间复杂度，简称为平均时间复杂度。

那如何分析平均时间复杂度呢，还是拿刚才那段查找函数来说：

要查找的变量 x 在数组中的位置，有 n+1 种情况：在数组的 0～n-1 位置中和不在数组中。然后把每种情况下，查找需要遍历的元素个数累加起来，然后再除以 n+1，就可以得到需要遍历的元素个数的平均值。

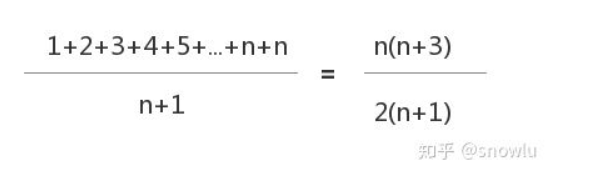
根据上章所说，时间复杂度的大 O 标记法中，可以省略掉系数、低阶、常量，所以，把这个公式简化之后，得到的平均时间复杂度就是 O(n)。

但是上面计算的过程中，没有考虑到概率的问题，因为出现在每个位置的概率是不一样的，所以得重新计算，如下分析：

要查找的变量 x，要么在数组里，要么就不在数组里。简单标记这两种情况下的概率都为 1/2。另外，要查找的数据出现在 0～n-1 这 n 个位置的概率也是一样的，为 1/n。所以，根据概率乘法法则，要查找的数据出现在 0～n-1 中任意位置的概率就是 1/(2n)。那我们把每种情况发生的概率都考虑进去，计算表达式就变成了：

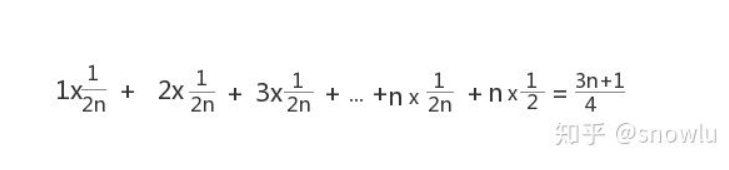
最后的结果也叫做概率中的加权平均值，那最后此段函数的平均时间复杂度就为 O(n)。

这么看，平均时间复杂度是不是好麻烦，还需要概率计算。实际上，在大多数情况下，我们并不需要区分最好、最坏、平均情况时间复杂度三种情况。很多时候，我们使用一个复杂度就可以满足需求了。只有同一块代码在不同的情况下，时间复杂度有量级的差距，我们才会使用这三种复杂度表示法来区分。

均摊情况

{
  var arr = new Array(n); // n 代表任意数字
  var ind = 0;
  function add(num) {
    if (ind === arr.length) {
      var sum = 0;
      for (var i = 0; i < arr.length; i++) {
        sum += arr[i];
      }
      arr[0] = sum;
      ind = 1;
    }
    arr[ind] = num;
    ind++;
  }
}

add 函数就是实现一个往数组中添加数据的功能。先定义一个任意长度的空数组，然后给数组添加数据。当达到数组长度后，也就是 ind === array.length 时，用 for 循环遍历数组求和，将求和之后的 sum 值放到数组的第一个位置，然后再将新的数据插入。但如果数组一开始就有空的话，则直接将数据添加到数组中。

来分析下此函数的时间复杂度：

最理想的情况下，数组中有剩余位置，我们只需要将数据添加到数组下标为 ind 的位置就可以了，所以最好情况时间复杂度为 O(1)。最糟糕的情况下，数组中没有剩余位置，我们需要先做一次数组的遍历求和，然后再添加数据，所以最坏情况时间复杂度为 O(n)。

接下来分析需要计算的 平均时间复杂度：

由于数组的长度是 n，根据数据添加的位置的不同，可以分为 n 种情况，每种情况的时间复杂度是 O(1)。除此之外，还有一种特殊的情况，就是在数组没有空闲空间时添加一个数据，这个时候的时间复杂度是 O(n)。而且，这 n+1 种情况发生的概率一样，都是 1/(n+1)。
$\frac{n + n}{n + 1}$
所以根据大 O 表示法，平均时间复杂度就为 O(1)。

其实 add 函数的平均复杂度不需要这么复杂，接下来我们看看 find 函数和 add 函数的区别：

find 函数在极端情况下，时间复杂度才为 O(1)。但 add 函数在大部分情况下，时间复杂度都为 O(1)。只有个别情况下，时间复杂度才比较高，为 O(n)。
对于 add 函数来说，O(1) 时间复杂度的添加和 O(n) 时间复杂度的添加，出现的频率是非常有规律的，而且有一定的前后顺序，一般都是一个 O(n) 添加之后，紧跟着 n-1 个 O(1) 的添加操作，循环往复。

所以，针对这样一种特殊场景的复杂度分析，我们并不需要像之前讲平均复杂度分析方法那样，找出所有的输入情况及相应的发生概率，然后再计算加权平均值。

针对这种特殊的情况，我们引入了一种更加简单的分析方法：摊还分析法。通过摊还分析得到的时间复杂度，叫 均摊时间复杂度。

那如何使用摊还分析法来分析算法的均摊时间复杂度呢？

还是看 add 函数。每一次 O(n) 的添加操作，都会跟着 n-1 次 O(1) 的添加操作，所以把耗时多的那次操作均摊到接下来的 n-1 次耗时少的操作上，均摊下来，这一组连续的操作的均摊时间复杂度就是 O(1)。这就是均摊分析的大致方法。

一般情况总结为：

对一个数据结构进行一组连续操作中，大部分情况下时间复杂度都很低，只有个别情况下时间复杂度比较高，而且这些操作之间存在前后连贯的时序关系，这个时候，我们就可以将这一组操作放在一块儿分析，看是否能将较高时间复杂度那次操作的耗时，平摊到其他那些时间复杂度比较低的操作上。而且，在能够应用均摊时间复杂度分析的场合，一般均摊时间复杂度就等于最好情况时间复杂度。

生活举例

今天你准备去老王家拜访下，可惜老王的爱人叫他去打个酱油，她告诉你说她限时 n 分钟给他去买。
那么你想着以他家到楼下小卖部来回最多一分钟，那么 “最好的情况”就是你只用等他一分钟。
那么也有可能遇到突发情况，比如说电梯没电了，或者路上摔了一跤，天知道他去干了什么，用了 n 分钟。没办法，老婆有令，n 分钟限时，那这就是“最坏的情况”。
那“平均时间复杂度” 就是他有可能是第 1,2,3,...,n 中的某个分钟回来，那平均就是 1+2+3+...n/n，把所有可能出现的情况的时间复杂度相加除以情况数。
“均摊时间复杂度”的话就是把花时间多的分给花时间少的，得到一个中间值。假如 n 是 10 分钟，那么 9 分钟分 4 分钟到 1 分钟那，8 分 3 给 2...，那均摊下来就是 5 分钟。

四种复杂度

同一段代码在不同情况下时间复杂度会出现量级差异，为了更全面，更准确的描述代码的时间复杂度，所以引入这 4 个概念。
代码复杂度在不同情况下出现量级差别时才需要区别这四种复杂度。大多数情况下，是不需要区别分析它们的。

常见算法复杂度

数据结构

图

排序算法

搜索算法

算法名词

山脉数组

所谓山脉数组，即数组 A 假如是一个山脉数组的话，需要满足如下条件：
首先，A.length >= 3
其次，在 0 < i < A.length - 1 条件下，存在 i 使得：
- A[0] < A[1] < ... A[i-1] < A[i]
- A[i] > A[i+1] > ... > A[A.length - 1]

归纳推理

归纳推理的理解

若将问题的规模降到 0，即已知 A~0~，很容易证明，则有： $A_{0} \to B$
同时，考察从 A~0~增加一个元素，得到 A~1~的变化过程，即： $A_{0} \to A_{1}$
- 进一步考察 $A_{1} \to A_{2}, A_{2} \to A_{3}, . . ., A_{i} \to A_{i + 1}$
这种方法是（严格的）归纳推理，常常被称作数学归纳法
此时，由于上述推导往往不是等价推导（ $A_{i}$ 和 $A_{i + 1}$ 不是互为充要条件），导致随着 i 的增加，有价值的信息越来越少，为了避免这一问题，采取如下方案：
- ${A_{1}} \to A_{2}, {A_{1} A_{2}} \to A_{3}, . . ., {A_{1} A_{2} . . . A_{i}} \to A_{i + 1}$
修正后的方法，依然是（严格的）归纳推理，被称为第二数学归纳法

基本归纳法

基本归纳法：对于 $A_{i + 1}$ ，只需要考察前一个状态 $A_{i}$ 即可完成整个推理过程，它的特点是只要状态 $A_{i}$ 确定，则计算 $A_{i + 1}$ 时不需要考虑更前序的状态，在图论中，常常称之为马尔可夫模型，马尔科夫链
在计算机算法中，马尔可夫模型往往对应着贪心算法

高阶归纳法

相应的，对于 $A_{i + 1}$ ，需要考察前序状态集才可以完成推理的，我们称之为高阶马尔可夫模型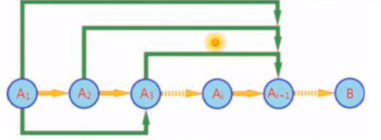
高阶马尔可夫模型，对应着动态规划

无后效性

无论是动态规划还是贪心算法，都是根据 A[0...i] 计算 A[i+1] 的过程
- 计算 A[i+1] 不需要 A[i+2]``A[i+3]
- 一旦完成计算 A[i+1]，后面再计算 A[i+2]，A[i+3] 时不会更改 A[i+1] 的值
这就是无后效性
可以这样理解动态规划，计算 A[i+1] 只需要知道 A[0...i] 的值即可，无需知道 A[0...i] 是通过何种途径得到的。如果将 A[0...i] 当作是一个整体，则可以认为动态规划是马尔可夫模型，而不是高阶马尔可夫模型