knapsack-problem

#review

https://segmentfault.com/a/1190000012829866/

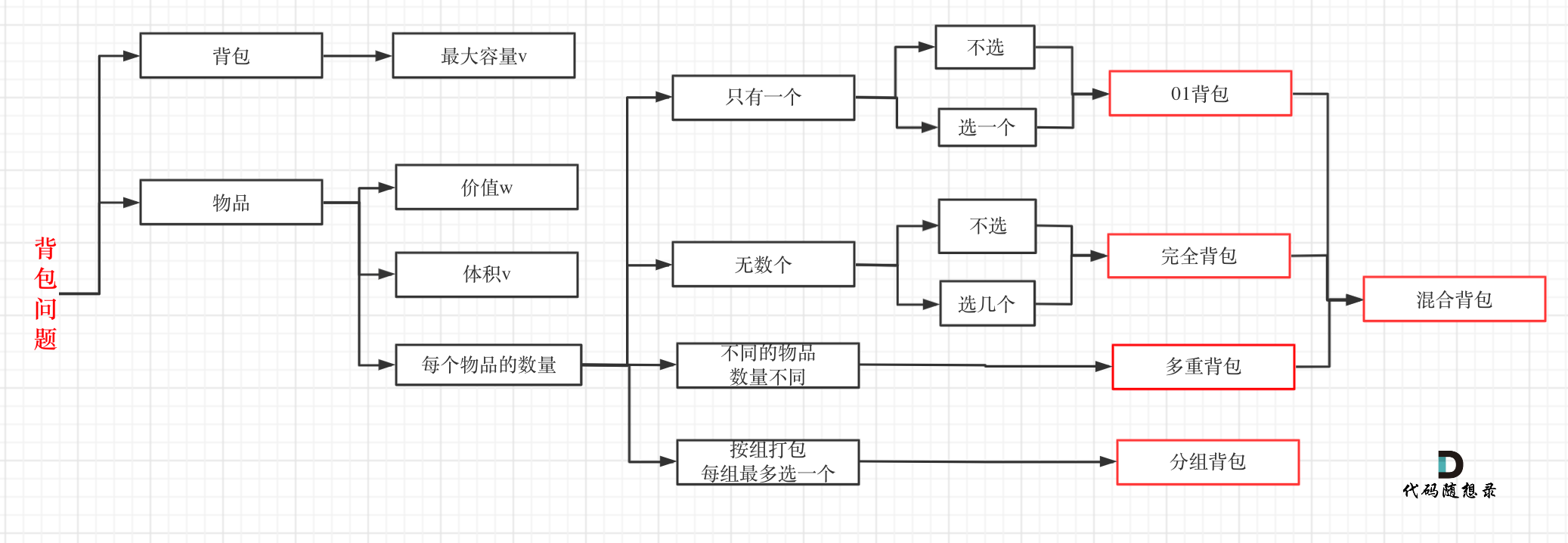
对于面试的话，其实掌握 01 背包，和完全背包，就够用了，最多可以再来一个多重背包。

至于背包九讲其其他背包，面试几乎不会问，都是竞赛级别的了，leetcode 上连多重背包的题目都没有，所以题库也告诉我们，01 背包和完全背包就够用了。

而完全背包又是也是 01 背包稍作变化而来，即：完全背包的物品数量是无限的。

所以背包问题的理论基础重中之重是 01 背包，一定要理解透

01 背包问题

问题描述：

有 $n$ 件物品和 $1$ 个容量为 W 的背包。每种物品均只有一件，第 $i$ 件物品的重量为 $w e i g h t s [i]$ ，价值为 $v a l u e s [i]$ ，求解将哪些物品装入背包可使价值总和最大。

对于一种物品，要么装入背包，要么不装。所以对于一种物品的装入状态只是 0 或 1, 此问题称为01 背包问题

问题分析：

数据：物品个数 $n = 5$ ,物品重量 $w e i g h t s = [2 ， 2 ， 6 ， 5 ， 4]$ ,物品价值 $v a l u e s = [6 ， 3 ， 5 ， 4 ， 6]$ ,背包总容量 $W = 10$ 。

我们设置一个矩阵 $f$ 来记录结果， $f (i, j)$ 表示可选物品为 $o . . . i$ 背包容量为 $j (0 <= j <= W)$ 时，背包中所放物品的最大价值。

w	v	i\j
2	6	0
2	3	1
6	5	2
5	4	3
4	6	4

第一行

我们先看第一行，物品 0 的体积为 2，价值为 6：

当容量为 0 时，什么也放不下，因此第一个格式只能填 0，程序表示为 $f (0, 0) = 0$
当 $j = 1$ 时，依然放不下 $w_{0}$ ，因此依然为 0， $f (0, 1) = 0$
当 $j = 2$ 时，能放下 $w_{0}$ ，于是有 $f (0, 2) = v_{0} = 6$
当 $j = 3$ 时，也能放下 $w_{0}$ ，但我们只有一个物品 0，因此它的值依然是 6
于是一直到 $j = 10$ 时，它的值都是 $v_{0}$

并不需要进行排序，因为参考的时候无论顺序与否都是当前组合的最佳选择

w	v	i\j	0	1	2	3	4	5	6	7	8	9	10
2	6	0	0	0	6	6	6	6	6	6	6	6	6
2	3	1
6	5	2
5	4	3
4	6	4

根据第一行，我们得到如下方程

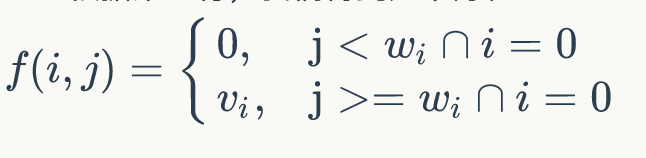
当背包容量少于物品价值时，总价值为 0，否则为物品的价值

第二行

然后我们看第二行，确定 $f (0, 1. . .10)$ 这 11 个元素的值。

当 $j = 0$ 时，依然什么也放不下，值为 0，但我们发觉它是上方格式的值一样的， $f (1, 0) = 0$
当 $j = 1$ 时，依然什么也放不下，值为 0，但我们发觉它是上方格式的值一样的， $f (1, 1) = 0$
当 $j = 2$ 时，它可以选择放入物品 1 或不放。
- 如果选择不放物品 1，背包里面有物品 0，最大价值为 6。
- 如果选择放入物品 1，我们要用算出背包放入物品 1 后还有多少容量，然后根据容量查出它的价值，再加上物品 1 的价值，即 $f (0, j - w_{1}) + v_{1}$ 。由于我们的目标是尽可能装最值钱的物品，因此放与不放，我们需要通过比较来决定，于是有 $f (i, j) = m a x f (0, j), f (0, j - w_{1}) + v_{1}$
显然 $v_{1} = 2 ， v_{0} = 6$ , 因此这里填 $v_{0}$ 。

从比较的这一步可以看出，不需要对价值进行排序，因为无论如何在当前可以选择的组合中，比较后都可以选择最佳选择

当 $j = 3$ 时，情况相同。
当 $j = 4$ ，能同时放下物品 0 与物品 1，我们这个公式的计算结果也合乎我们的预期，得到 $f (1, 4) = 9$ 。
当 $j > 4$ 时，由于背包只能放物品 0 与物品 1，那么它的最大价值也一直停留在 $v_{0} + v_{1} = 9$

w	v	i\j	0	1	2	3	4	5	6	7	8	9	10
2	6	0	0	0	6	6	6	6	6	6	6	6	6
2	3	1	0	0	6	6	9	9	9	9	9	9	9
6	5	2
5	4	3
4	6	4

从第二行, 我们可以得出 f(i,j)=max{f(0,j),f(0,j-w_1)+v_1

第三行

当 $j = 0$ 时，什么都放不下， $f (2, 0) = 0$
当 $j = 1$ 时，依然什么也放不下， $f (2, 1) = 0$
当 $j = 2$ 时，虽然放不下 $w_{2}$ ，但我们根据上表得知这个容号时，背包能装下的最大价值是 6。
继续计算下去，其实与上面推导的公式结果是一致的，说明公式是有效的。
当 $j = 8$ 时，背包可以是放物品 0、1，或者放物品 1、2，或者放物品 0、2。物品 0、1 的价值，我们在表中就可以看到是 9，至于其他两种情况我们姑且不顾，我们目测就知道是最优值是 $6 + 5 = 11$ ，恰恰我们的公式也能正确计算出来。
当 $j = 10$ 时,刚好三个物品都能装下，它们的总值为 14，即 $f (2, 10) = 14$

w	v	i\j	0	1	2	3	4	5	6	7	8	9	10
2	6	0	0	0	6	6	6	6	6	6	6	6	6
2	3	1	0	0	6	6	9	9	9	9	9	9	9
6	5	2	0	0	6	6	9	9	9	9	11	11	14
5	4	3
4	6	4

整理一下第 1，2 行的适用方程：

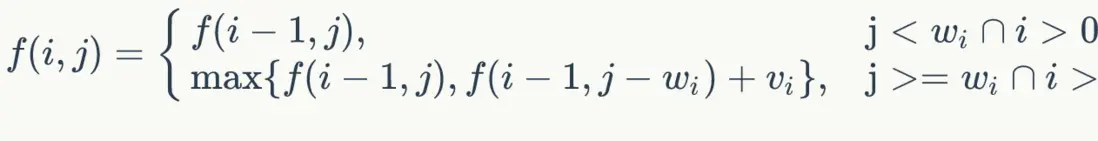
我们根据此方程，继续计算下面各列，于是得到

w	v	i\j	2	3	4	5	6	7	8	9	10
2	6	0	6	6	6	6	6	6	6	6	6
2	3	1	6	6	9	9	9	9	9	9	9
6	5	2	6	6	9	9	9	9	11	11	14
5	4	3	6	6	9	9	9	10	11	13	14
4	6	4	6	6	9	9	12	12	15	15	15

至此，我们就可以得到解为 15.
我们最后根据 0-1 背包问题的最优子结构性质，建立计算 $f (i, j)$ 的递归式：

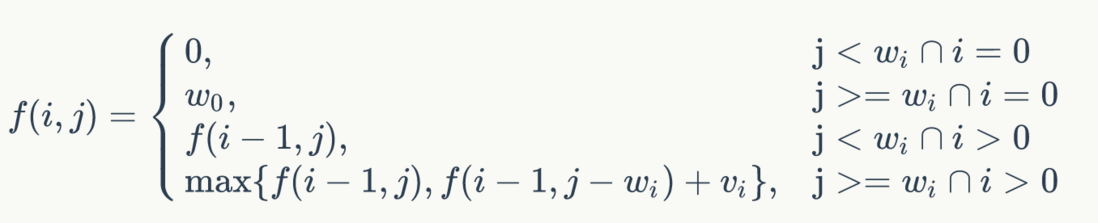
function knapsack(weights, values, W) {
    var n = weights.length - 1
    var f = [[]]
    for (var j = 0; j <= W; j++) {
        if (j < weights[0]) { 
	        //如果容量不能放下物品0的重量，那么价值为0
            f[0][j] = 0
        } 
        else {
            //否则等于物体0的价值
            f[0][j] = values[0]
        }
    }
    for (var j = 0; j <= W; j++) {
        for (var i = 1; i <= n; i++) {
            if (!f[i]) { 
	            //创建新一行
                f[i] = []
            }
            if (j < weights[i]) { 
	            //等于之前的最优值
                f[i][j] = f[i - 1][j]
            } 
            else {
                f[i][j] = Math.max(f[i - 1][j], f[i - 1][j - weights[i]] + values[i])
            }
        }
    }
    return f[n][W]
}
var a = knapsack([2, 2, 6, 5, 4], [6, 3, 5, 4, 6], 10)

console.log(a)

各种优化：

合并循环

现在方法里面有两个大循环，它们可以合并成一个。

function knapsack(weights, values, W) {
    var n = weights.length;
    var f = new Array(n)
    for (var i = 0; i < n; i++) {
        f[i] = []
    }

    for (var i = 0; i < n; i++) {
        for (var j = 0; j <= W; j++) {
            if (i === 0) {
                //第一行
                f[i][j] = j < weights[i] ? 0 : values[i]
            } else {
                if (j < weights[i]) {
                    //等于之前的最优值
                    f[i][j] = f[i - 1][j]
                } else {
                    f[i][j] = Math.max(f[i - 1][j], f[i - 1][j - weights[i]] + values[i])
                }
            }
        }
    }
    return f[n - 1][W]
}

先遍历物品，然后遍历背包重量, 先遍历背包，再遍历物品，也是可以的

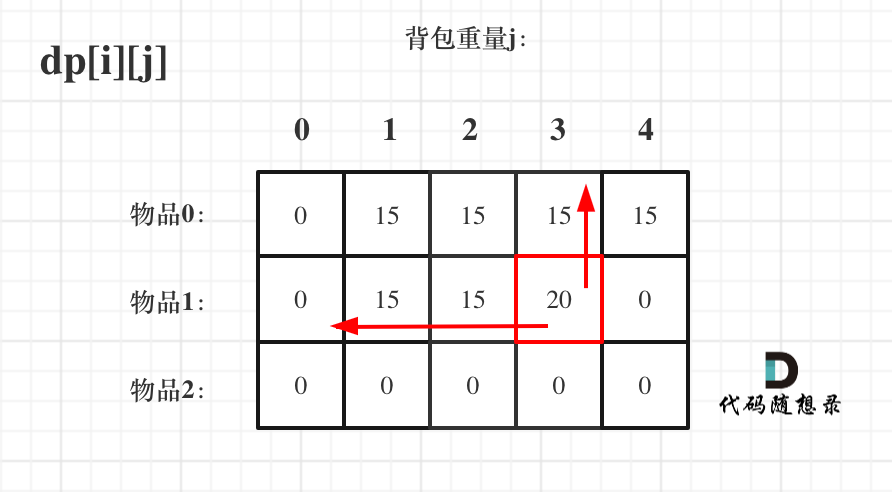
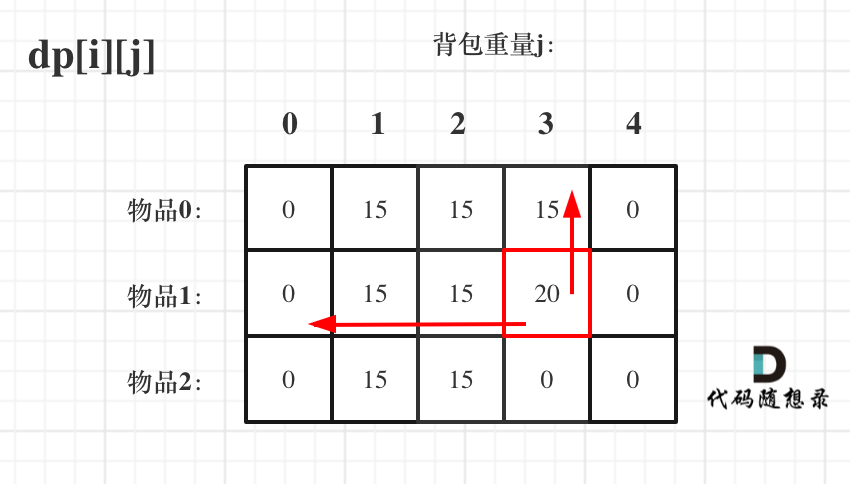
大家可以看出，虽然两个 for 循环遍历的次序不同，但是 dp[i][j] 所需要的数据就是左上角，根本不影响 dp[i][j] 公式的推导

但先遍历物品再遍历背包这个顺序更好理解。

初始化

然后我们再认真地思考一下，为什么要孤零零地专门处理第一行呢？f[i][j] = j < weights[i] ? 0 : values[i] 是不是能适用于下面这一行 f[i][j] = Math.max(f[i-1][j], f[i-1][j-weights[i]] + values[i])。Math.max 可以轻松转换为三元表达式，结构极其相似。而看一下 i-1 的边界问题，有的书与博客为了解决它，会添加第 0 行，全部都是 0，然后 i 再往下挪。其实我们也可以添加一个 $- 1$ 行。那么在我们的方程中就不用区分 $i == 0$ 与 $0 > 0$ 的情况，方程与其他教科书的一模一样了！

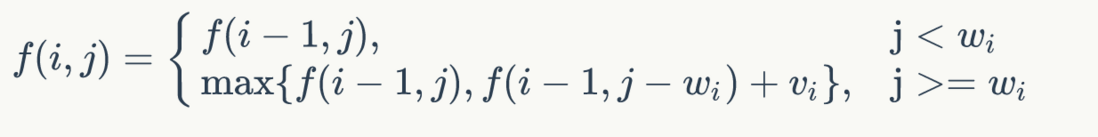
function knapsack(weights, values, W) {
    var n = weights.length;
    var f = new Array(n)
    //负1行，因为有W+1次内循环
    f[-1] = new Array(W + 1).fill(0)
    for (var i = 0; i < n; i++) {
        //注意边界，没有等号
        f[i] = new Array(W).fill(0)
        for (var j = 0; j <= W; j++) {
            //注意边界，有等号,因为重量等于10最大
            if (j < weights[i]) {
                //注意边界， 没有等号
                f[i][j] = f[i - 1][j]
            } else {
                //case 3
                f[i][j] = Math.max(f[i - 1][j], f[i - 1][j - weights[i]] + values[i]);
            }
        }
    }
    return f[n - 1][W]
}

w	v	i\j	2	3	4	5	6	7	8	9	10
X	X	-1	0	0	0	0	0	0	0	0	0	0
2	6	0	6	6	6	6	6	6	6	6	6
2	3	1	6	6	9	9	9	9	9	9	9
6	5	2	6	6	9	9	9	9	11	11	14
5	4	3	6	6	9	9	9	10	11	13	14
4	6	4	6	6	9	9	12	12	15	15	15

负一行的出现可以大大减少了在双层循环的分支判定。是一个很好的技巧。

注意，许多旧的教程与网上文章，通过设置二维数组的第一行为 0 来解决 i-1 的边界问题（比如下图）。当然也有一些思维转不过来的缘故，他们还在坚持数字以 1 开始，而我们新世代的 IT 人已经确立从 0 开始的编程思想。

使用滚动数组压缩空间

所谓滚动数组，目的在于优化空间，因为目前我们是使用一个 $i * j$ 的二维数组来储存每一步的最优解。在求解的过程中，我们可以发现，当前状态只与前一行的状态有关，那么更之前存储的状态信息已经无用了，可以舍弃的，我们只需要存储当前状态和前一行状态，所以只需使用 $2 * j$ 的空间，循环滚动使用，就可以达到跟 $i * j$ 一样的效果。这是一个非常大的空间优化。

currentLine 和 referLine 分别对应着 dp[i] 和 dp

  function knapsack(weights, values, W) {
    const n = weights.length
    let lineA = new Array(W+1).fill(0)
    let lineB = new Array(W+1).fill(0)
    let referLine = lineA
    let currentLine = lineB
    for (let i = 0; i < n; i++) {
      for (let j = 0; j <= W; j++) {
        if (j < weights[i]) {
          // f[i][j] = f[i-1][j]
          currentLine[j] = referLine[j]
        } else {
          // f[i][j] = Math.max(f[i - 1][j], f[i - 1][j - weights[i]] + values[i])
          currentLine[j] = Math.max(referLine[j],referLine[j-weights[i]]+values[i])
        }
      }
      // 内循环结束，更新了一行，当前和参考互换
      const aux = referLine
      referLine = currentLine
      currentLine = aux
      // currentLine = new Array(W+1).fill(0) 没有真正的减小空间复杂度
      // [referLine,currentLine] = [currentLine,referLine] Cannot set property '[object Array]' of undefined
      // ;([referLine,currentLine] = [currentLine,referLine]) 可以正确解析
    }
    console.log(referLine)
    return referLine[W]
  }
  
  var a = knapsack([2,3,4,1],[2,5,3, 2],5)
  console.log(a)
  var b = knapsack([2,2,6,5,4],[6,3,5,4,6],10)
  console.log(b)

我们还可以用更 hack 的方法代替 currLine, lastLine

  function knapsack(weights, values, W){
      var n = weights.length
     
      var f = [new Array(W+1).fill(0),[]], now = 1, last //case1 在这里使用es6语法预填第一行
      for(var i = 0; i < n; i++){ 
          for(var j=0; j<=W; j++){
              f[now][j] = f[1-now][j] //case2 等于另一行的同一列的值
              if( j>= weights[i] ){                         
                  var a = f[1-now][j]
                  var b = f[1-now][j-weights[i]] + values[i]
                  f[now][j] = Math.max(a, b);//case3
              }
           }
           last = f[now]
           now = 1-now // 1 - 0 => 1;1 - 1 => 0; 1 - 0 => 1 ....
     }
     return last[W];
  }
  var a = knapsack([2,3,4,1],[2,5,3, 2],5)
  console.log(a)
  var b = knapsack([2,2,6,5,4],[6,3,5,4,6],10)
  console.log(b)

注意，这种解法由于丢弃了之前 N 行的数据，因此很难解出挑选的物品，只能求最大价值。

使用一维数组压缩空间

观察我们的状态迁移方程:

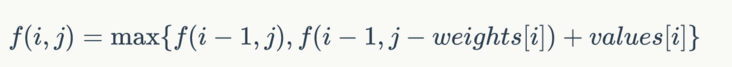
weights 为每个物品的重量，values 为每个物品的价值，W 是背包的容量，i 表示要放进第几个物品，j 是背包现时的容量（假设我们的背包是魔术般的可放大，从 0 变到 W）。

我们假令 i = 0

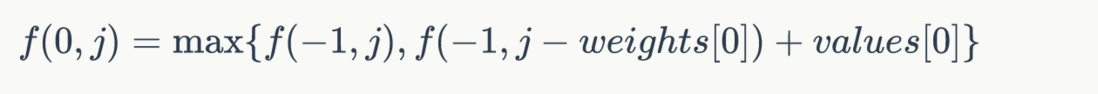
f 中的 -1 就变成没有意义，因为没有第 -1 行，而 weights[0], values[0] 继续有效， $f (0, j)$ 也有意义，因为我们全部放到一个一维数组中。于是:

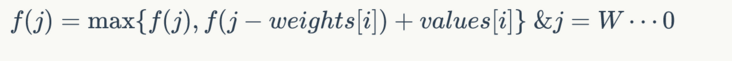
这方程后面多加了一个限制条件，要求是从大到小循环。为什么呢？

假设有物体 $z$ 容量 2，价值 $v_{z}$ 很大，背包容量为 5，如果 j 的循环顺序不是逆序，那么外层循环跑到物体 $z$ 时，内循环在 $j = 2$ 时， $z$ 被放入背包。当 $j = 4$ 时，寻求最大价值，物体 z 放入背包， $f (4) = m a x (f (4), f (2) + v_{z})$ ，这里毫无疑问后者最大。但此时 $f (2) + v_{z}$ 中的 $f (2)$ 已经装入了一次 $z$ ，这样一来 $z$ 被装入两次不符合要求，如果逆序循环 j，这一问题便解决了。

从后面往前方参考的是没有修改过的上一行，本质上是不断的修改同一行

dp[i][j] 表示从下标为 [0-i] 的物品里任意取，放进容量为 j 的背包，价值总和最大是多少

在一维 dp 数组中，dp[j] 表示：容量为 j 的背包，所背的物品价值可以最大为 dp[j]

实际上一维数组的含义是在动态变化的, 在可选物品为 [0-i] 时, dp[j] 表示：容量为 j 的背包，所背的物品价值可以最大为 dp[j]

function knapsack(weights, values, W) {
    var n = weights.length;
    var dp = new Array(W + 1).fill(0)
    for (var i = 0; i < n; i++) {
        // j<weight[i]的与上一轮相等
        for (var j = W; j >= weights[i]; j--) {
            // dp[j] 即是不放入 weights[i]
            // dp[j - weights[i]] + values[i] 即是放入 weights[i]
            dp[j] = Math.max(dp[j], dp[j - weights[i]] + values[i]);
        }
        console.log(dp.concat()) //调试
    }
    return dp[W];
}
var b = knapsack([2, 2, 6, 5, 4], [6, 3, 5, 4, 6], 10)
console.log(b)

一维数组先遍重量再遍历物品

从横着的一行, 变成了竖着的一列, 同样是需要从后往前遍历, 才能保证数据是上一次的, 避免重复

此时 dp[j] 的含义是什么呢? 可以选择所有物品, 在 j 背包重量下, 最大的价值是多少

01 背包, 一维数组最重要的特点就是参考的值是上一行的, 所以需要倒序遍历

那么 j 依然是倒序, 相当于在第一轮 for 循环结束时要求的就已经是: 在背包容量为 9, 可选的物品为所有物品时最大的价值. 相当于要在第一层 for 循环就求出答案了, 显然是不可能的.

那么只能是让 j 顺序增大, 顺序遍历的话又导致上一列的内容被覆盖了, 参考的值会越变越大

所以还是不行, 一维数组不能调换 for 循环的顺序

所以 dp[j] 的含义不能这样定了, 得改改. 改成类似 dp[i] 的概念, 但是 dp[i] 没有办法参考已有的值? 或者说参考形式不能是 dp[j -nums[i]] 的这种形式, 但是也找不到其他状态转移方程了, 所以 dp[j] 的含义是改不了的.

状态转移方程约束了我们只能以重量作为 j 的含义

在背包容量为 9, 可选的物品为所有物品时最大的价值
在背包容量为 8, 可选的物品为所有物品时最大的价值
容量增大, 没有办法参考前面的数组, 无法建立状态转移方程

选择物品

上面讲解了如何求得最大价值，现在我们看到底选择了哪些物品，这个在现实中更有意义。许多书与博客很少提到这一点，就算给出的代码也不对，估计是在设计状态矩阵就出错了。

仔细观察矩阵，从 $f (n - 1, W)$ 逆着走向 $f (0, 0)$ ，设 i=n-1,j=W，如果 $f (i, j)$ === $f (i - 1, j - w_{i}) + v_{i}$

说明包里面有第 i 件物品，因此我们只要当前行不等于上一行的总价值，就能挑出第 i 件物品，然后 j 减去该物品的重量，一直找到 j = 0 就行了。

  function knapsack(weights, values, W){
      var n = weights.length;
      var f = new Array(n)
      f[-1] = new Array(W+1).fill(0)
      var selected = [];
      for(var i = 0 ; i < n ; i++){ //注意边界，没有等号
          f[i] = [] //创建当前的二维数组
          for(var j=0; j<=W; j++){ //注意边界，有等号
              if( j < weights[i] ){ //注意边界， 没有等号
                  f[i][j] = f[i-1][j]//case 1
              }else{
                  f[i][j] = Math.max(f[i-1][j], f[i-1][j-weights[i]]+values[i]);//case 2
              }
          }
      }
      var j = W, w = 0
      for(var i=n-1; i>=0; i--){
           if(f[i][j] > f[i-1][j]){
               selected.push(i)
               console.log("物品",i,"其重量为", weights[i],"其价格为", values[i])
               j = j - weights[i];
               w +=  weights[i]
           }
       }
      console.log("背包最大承重为",W," 现在重量为", w, " 总价值为", f[n-1][W])
      return [f[n-1][W], selected.reverse() ]
  }
  var a = knapsack([2,3,4,1],[2,5,3, 2],5)
  console.log(a)
  var b = knapsack([2,2,6,5,4],[6,3,5,4,6],10)
  console.log(b)

递归法解 01 背包

由于这不是动态规则的解法，大家多观察方程就理解了：

  function knapsack(n, W, weights, values, selected) {
      if (n == 0 || W == 0) {
          //当物品数量为0，或者背包容量为0时，最优解为0
          return 0;
      } else {
          //从当前所剩物品的最后一个物品开始向前，逐个判断是否要添加到背包中
          for (var i = n - 1; i >= 0; i--) {
              //如果当前要判断的物品重量大于背包当前所剩的容量，那么就不选择这个物品
              //在这种情况的最优解为f(n-1,C)
              if (weights[i] > W) {
                  return knapsack(n - 1, W, weights, values, selected);
              } else {
                  var a = knapsack(n - 1, W, weights, values, selected); //不选择物品i的情况下的最优解
                  var b = values[i] + knapsack(n - 1, W - weights[i], weights, values, selected); //选择物品i的情况下的最优解
                  //返回选择物品i和不选择物品i中最优解大的一个
                  if (a > b) {
                      selected[i] = 0; //这种情况下表示物品i未被选取
                      return a;
                  } else {
                      selected[i] = 1; //物品i被选取
                      return b;
                  }
              }
          }
      }
  }        
  var selected = [], ws = [2,2,6,5,4], vs = [6,3,5,4,6]
  var b = knapsack( 5, 10, ws, vs, selected)
  console.log(b) //15
  selected.forEach(function(el,i){
      if(el){
          console.log("选择了物品"+i+ " 其重量为"+ ws[i]+" 其价值为"+vs[i])
      }
  })

题目

01 背包：416. 分割等和子集 474. 一和零 494. 目标和 879. 盈利计划 1049. 最后一块石头的重量 II 1230. 抛掷硬币

完全背包：1449. 数位成本和为目标值的最大数字 322. 零钱兑换 518. 零钱兑换 II 279. 完全平方数

欢迎补充

File	difficulty	etags	date-created
1049. 最后一块石头的重量 II	medium	#leetcode/dp/knapsack/0-1 #leetcode/unsolved	2023-07-11-Tue, 8:02:47 pm
416. 分割等和子集	medium	#leetcode/dp/knapsack/0-1 #leetcode/unsolved	2023-07-11-Tue, 6:47:18 pm
474. 一和零	medium	#leetcode/dp/knapsack/0-1 #leetcode/recursive/memo	2023-07-12-Wed, 8:40:02 pm
494. 目标和	medium	#leetcode/dp/knapsack/0-1 #leetcode/dp/combination #leetcode/backtracking/combination #leetcode/unsolved	2023-07-12-Wed, 6:43:08 pm

完全背包问题

问题描述：

有 $n$ 件物品和 $1$ 个容量为 W 的背包。每种物品没有上限，第 $i$ 件物品的重量为 $w e i g h t s [i]$ ，价值为 $v a l u e s [i]$ ，求解将哪些物品装入背包可使价值总和最大。

问题分析：

最简单思路就是把完全背包拆分成 01 背包，就是把 01 背包中状态转移方程进行扩展，也就是说 01 背包只考虑放与不放进去两种情况，而完全背包要考虑放 0、放 1、放 2...的情况，

这个 k 当然不是无限的，它受背包的容量与单件物品的重量限制，即 $j / w e i g h t s [i]$ 。假设我们只有 1 种商品，它的重量为 20，背包的容量为 60，那么它就应该放 3 个，在遍历时，就 0、1、2、3 地依次尝试。

程序需要求解 $n * W$ 个状态，每一个状态需要的时间为 $O （ W / w_{i} ）$ ，总的复杂度为 $O (n W * Σ (W / w_{i}))$ 。

我们再回顾 01 背包经典解法的核心代码

  for(var i = 0 ; i < n ; i++){ 
     for(var j=0; j<=W; j++){ 
         f[i][j] = Math.max(f[i-1][j], f[i-1][j-weights[i]]+values[i]))
        }
     }
  }

现在多了一个 k，就意味着多了一重循环

  for(var i = 0 ; i < n ; i++){ 
     for(var j=0; j<=W; j++){ 
         for(var k = 0; k < j / weights[i]; k++){
            f[i][j] = Math.max(f[i-1][j], f[i-1][j-k*weights[i]]+k*values[i]))
          }
        }
     }
  }

考虑硬币最少找零的问题，因为价值是递增，所以直接全部塞满，剩下的再参考上一行，但是这里价值不一定是递增的，所以需要多一层循环，来判断，超出 k 的个数变动中价值最高的那个 f[i][j]

function completeKnapsack(weights, values, W){
    var f = [], n = weights.length;
    f[-1] = [] //初始化边界
    for(var i = 0; i <= W; i++){
        f[-1][i] = 0
    }
    for (var i = 0;i < n;i++){
        f[i] = new Array(W+1)
        for (var j = 0;j <= W;j++) {
            f[i][j] = 0;
            var bound = j / weights[i];
            for (var k = 0;k <= bound;k++) {
                f[i][j] = Math.max(f[i][j], f[i - 1][j - k * weights[i]] + k * values[i]);
            }
        }
    }
    return f[n-1][W];
}
//物品个数n = 3，背包容量为W = 5，则背包可以装下的最大价值为40.
var a = completeKnapsack([3,2,2],[5,10,20], 5) 
console.log(a) //40

O(nW) 优化

以下的讨论都是基于二维 dp 数组的, 所以 i - 1 代表上一行.

我们再进行优化，改变一下 f 思路，让 $f (i, j)$ 表示出在前 i 种物品中选取若干件物品放入容量为 j 的背包所得的最大价值。

所以说，对于第 i 件物品有放或不放两种情况，而放的情况里又分为放 1 件、2 件、...... $j / w_{i}$ 件

如果不放, 那么 $f (i, j) = f (i - 1, j)$ ；取上一行的

如果放，那么当前背包中应该出现至少一件第 i 种物品，所以 f(i,j) 中至少应该出现一件第 i 种物品,即 $f (i, j) = f (i, j - w_{i}) + v_{i}$ ，为什么会是 $f (i, j - w_{i}) + v_{i}$ ？

因为我们要把当前物品 i 放入包内，因为物品 i 可以无限使用，所以要用 $f (i, j - w_{i})$ ；
如果我们用的是 $f (i - 1, j - w_{i})$ ， $f (i - 1, j - w_{i})$ 的意思是说，我们只有一件当前物品 i，所以我们在放入物品 i 的时候需要考虑到第 i-1 个物品的价值 $f (i - 1, j - w_{i})$ ；
但是现在我们有无限件当前物品 i，我们不用再考虑第 i-1 个物品了，我们所要考虑的是在当前容量下是否再装入一个物品 i，而 $(j - w_{i})$ 的意思是指要确保 $f (i, j)$ 至少有一件第 i 件物品，所以要预留 c(i) 的空间来存放一件第 i 种物品。总而言之，如果放当前物品 i 的话，它的状态就是它自己 "i"，而不是上一个 "i-1"。

只要参考同一行就好了，因为在同一行容量是递增的，k 的可能数量也是逐步增加的

所以说状态转移方程为：

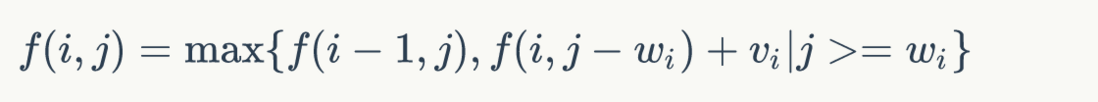
与 01 背包的相比，只是一点点不同，我们也不需要三重循环了

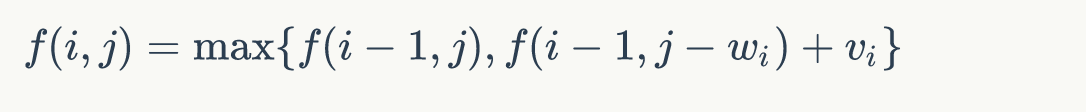
  function unboundedKnapsack(weights, values, W) {
      var f = [],
          n = weights.length;
      f[-1] = []; //初始化边界
      for (let i = 0; i <= W; i++) {
          f[-1][i] = 0;
      }
      for (let i = 0; i < n; i++) {
          f[i] = [];
          for (let j = 0; j <= W; j++) {
              if (j < weights[i]) {
                  f[i][j] = f[i - 1][j];
              } else {
                  f[i][j] = Math.max(f[i - 1][j], f[i][j - weights[i]] + values[i]);
              }
          }
          console.log(f[i].concat());//调试
      }
      return f[n - 1][W];
  }
  
  var a = unboundedKnapsack([3, 2, 2], [5, 10, 20], 5); //输出40
  console.log(a);
  var b = unboundedKnapsack([2, 3, 4, 7], [1, 3, 5, 9], 10); //输出12
  console.log(b);

我们可以继续优化此算法，可以用一维数组写

我们用 $f (j)$ 表示当前可用体积 j 的价值，我们可以得到和 01 背包一样的递推式：

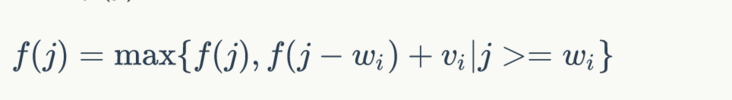
  function unboundedKnapsack(weights, values, W) {
    var n = weights.length,
      f = new Array(W + 1).fill(0);
    for (var i = 0; i < n; ++i) {
      // 因为完全背包只需要参考同一行的，所以不需要从尾到头覆写
      for (j = weights[i]; j <= W; ++j) {
        f[j] = Math.max(f[j], f[j - weights[i]] + values[i]);
      }
    }
    console.log(f)//调试
    return f[W];
  }
  var a = unboundedKnapsack([3, 2, 2], [5, 10, 20], 5); //输出40
  console.log(a);
  var b = unboundedKnapsack([2, 3, 4, 7], [1, 3, 5, 9], 10); //输出12
  console.log(b);

遍历顺序的讨论

遍历顺序

完全背包, 一维数组只能从小到大遍历, 因为要参考的是这一行的, 所以要让大的可以参考刚刚遍历过的小的

作为对比, 01 背包, 一维数组只能从大到小遍历, 因为要参考的是上一行的, 所以要让小的留着, 大的才可以参考

两个 for 循环的位置

可以调转, 01 背包中不能调转是因为 01 背包一维数组是从后往前遍历的, 不能根据多个物品的情况推出少数物品的情况, 而是要根据少数物品的情况, 推出多个物品的情况. 而在完全背包中, 一维数组是从前往后遍历的, 无论是从少物品开始, 还是从少重量开始, 都是可以正常参考的, 多的 case 参考少的 case

求方案数量

组合还是排列?

File	difficulty	etags	date-created
279. 完全平方数	medium	#leetcode/dp/knapsack/complete #leetcode/dp/combination #leetcode/backtracking/combination #leetcode/unsolved #leetcode/math/square	2023-07-13-Thu, 4:21:26 pm
322. 零钱兑换	medium	#leetcode/dp/knapsack/complete #leetcode/dp/combination #leetcode/backtracking/combination #leetcode/unsolved	2023-07-13-Thu, 3:52:39 pm
377. 组合总和 Ⅳ	medium	#leetcode/dp/knapsack/complete #leetcode/dp/combination #leetcode/backtracking/permutation #leetcode/unsolved	2023-07-13-Thu, 12:31:27 pm
494. 目标和	medium	#leetcode/dp/knapsack/0-1 #leetcode/dp/combination #leetcode/backtracking/combination #leetcode/unsolved	2023-07-12-Wed, 6:43:08 pm
518. 零钱兑换 II	medium	#leetcode/dp/knapsack/complete #leetcode/dp/combination #leetcode/backtracking/combination #leetcode/unsolved	2023-07-13-Thu, 10:30:11 am

零钱兑换II和爬楼梯问题到底有什么不同？

遍历顺序问题

物品和背包重量, 两个大的 for 循环, 研究遍历顺序的问题, 都是直接调换两个 for 循环的顺序即可, 因为条件不同, 所以更换 i 和 j 的位置意义有限

01 背包一维数组, 只能是先遍历物品, 再遍历重量

求方案数量时: 完全背包

如果求组合数就是外层 for 循环遍历物品，内层 for 遍历背包
如果求排列数就是外层 for 遍历背包，内层 for 循环遍历物品

还是回到 dp[j] 的定义本身, 在 target 为 j 时, 所能选择的方案总数

如果 j 在外层循环, 相当于是 j 固定了, 可选的硬币面额从 coins[0] 到 coins[n - 1]

因为外层循环是遍历从 1 到 target 的值，内层循环是遍历数组 nums 的值，在计算 dp[i] 的值时， nums 中的每个小于等于 i 的元素都可能作为元素之和等于 i 的排列的最后一个元素。例如， 1 和 3 都在数组 nums 中，计算 dp[4] 的时候，排列的最后一个元素可以是 1 也可以是 3，因此 dp[1] 和 dp[3] 都会被考虑到，即不同的顺序都会被考虑到。

如果把遍历 nums（物品）放在外循环，遍历 target 的作为内循环的话，举一个例子：计算 dp[4] 的时候，结果集只有 {1,3} 这样的集合，不会有{3,1}这样的集合，因为 nums 遍历放在外层，3 只能出现在 1 后面！

那 01 背包呢?

总结

问能否能装满背包（或者最多装多少）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ，对应题目如下：

问装满背包有几种方法：dp[j] += dp[j - nums[i]] ，对应题目如下：

问背包装满最大价值：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ，对应题目如下：

动态规划：474.一和零(opens new window)

问装满背包所有物品的最小个数：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ，对应题目如下：

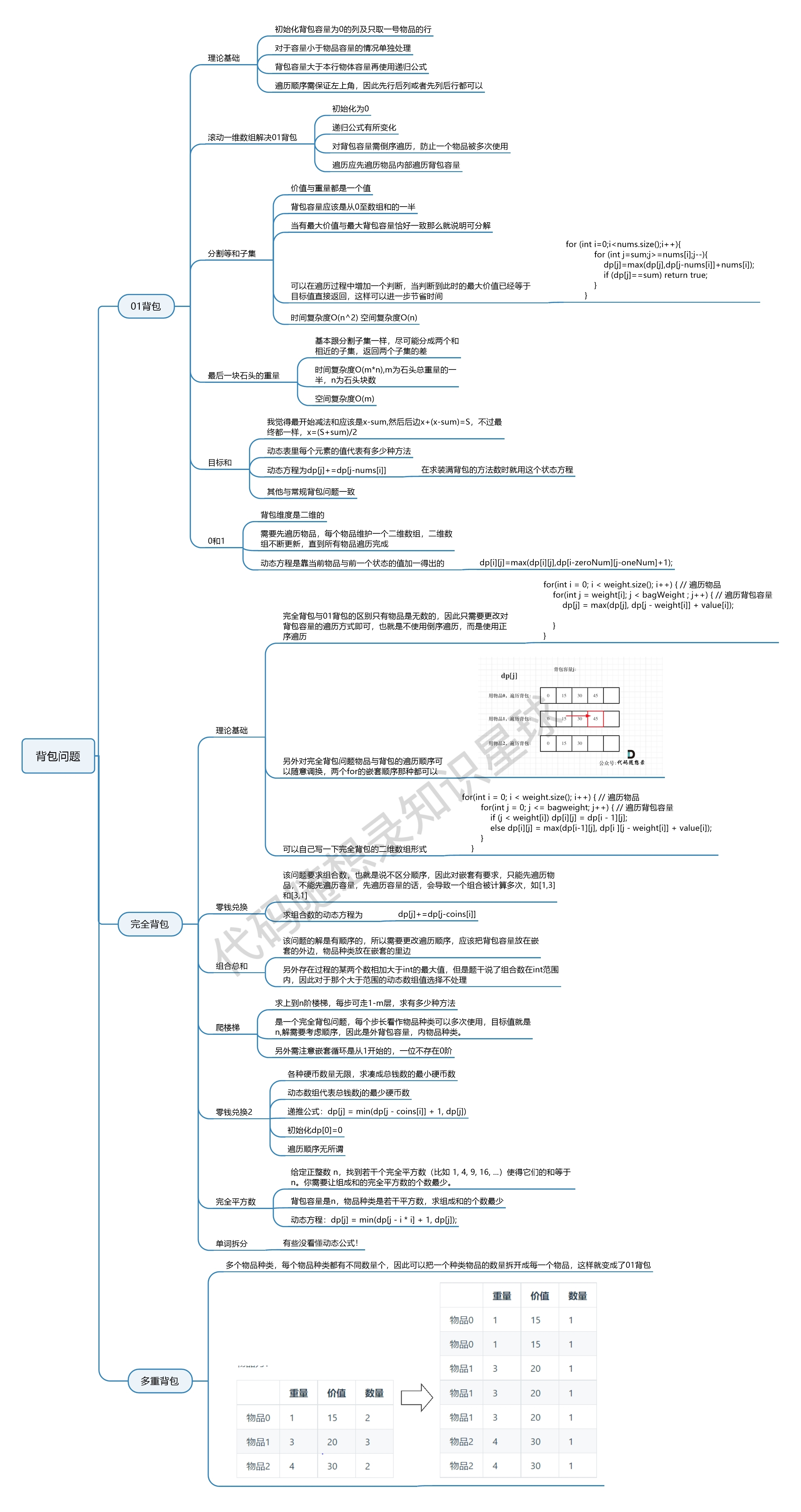
多重背包问题

问题描述：

有 $n$ 件物品和 $1$ 个容量为 W 的背包。每种物品最多有 numbers[i] 件可用，第 $i$ 件物品的重量为 $w e i g h t s [i]$ ，价值为 $v a l u e s [i]$ ，求解将哪些物品装入背包可使价值总和最大。

问题分析：

多重背包就是一个进化版完全背包。在我们做完全背包的第一个版本中，就是将它转换成 01 背包，然后限制 k 的循环

直接套用 01 背包的一维数组解法

function knapsack(weights, values, numbers, W) {
    var n = weights.length;
    var f = new Array(W + 1).fill(0)
    for (var i = 0; i < n; i++) {
        //其实就是把这类物品展开，调用numbers[i]次01背包代码
        for (var k = 0; k < numbers[i]; k++)
            //正常的01背包代码
            for (var j = W; j >= weights[i]; j--)
                f[j] = Math.max(f[j], f[j - weights[i]] + values[i]);
    }
    return f[W];
}
var b = knapsack([2, 3, 1], [2, 3, 4], [1, 4, 1], 6)
console.log(b)

使用二进制优化

其实说白了我们最朴素的多重背包做法是将有数量限制的相同物品看成多个不同的 0-1 背包。这样的时间复杂度为 $O (W * Σ n (i))$ , W 为空间容量，n(i) 为每种背包的数量限制。如果这样会超时，我们就得考虑更优的拆分方法，由于拆成 1 太多了，我们考虑拆成二进制数，对于 13 的数量，我们拆成 1，2，4，6（有个 6 是为了凑数）。 19 我们拆成 1，2，4，8，4 （最后的 4 也是为了凑和为 19）。经过这样的拆分我们可以组合出任意的小于等于 n(i) 的数目（二进制啊，必然可以）。j 极大程度缩减了等效为 0-1 背包时候的数量。大概可以使时间复杂度缩减为 $O (W * l o g (Σ N (i))$ ；

  定理：一个正整数n可以被分解成1,2,4,…,2^(k-1),n-2^k+1（k是满足n-2^k+1>0的最大整数）的形式，且1～n之内的所有整数均可以唯一表示成1,2,4,…,2^(k-1),n-2^k+1中某几个数的和的形式。
  
  证明如下：
  
  （1） 数列1,2,4,…,2^(k-1),n-2^k+1中所有元素的和为n，所以若干元素的和的范围为：[1, n]；
  
  （2）如果正整数t<= 2^k – 1,则t一定能用1,2,4,…,2^(k-1)中某几个数的和表示，这个很容易证明：我们把t的二进制表示写出来，很明显，t可以表示成n=a0*2^0+a1*2^1+…+ak*2^（k-1），其中ak=0或者1，表示t的第ak位二进制数为0或者1.
  
  （3）如果t>=2^k,设s=n-2^k+1，则t-s<=2^k-1，因而t-s可以表示成1,2,4,…,2^(k-1)中某几个数的和的形式，进而t可以表示成1,2,4,…,2^(k-1)，s中某几个数的和（加数中一定含有s）的形式。
  
  （证毕！）

  function mKnapsack(weights, values, numbers, W) {
      var kind = 0; //新的物品种类
      var ws = []; //新的物品重量
      var vs = []; //新的物品价值
      var n = weights.length;
      /**
       * 二进制分解
       * 100=1+2+4+8+16+32+37，观察可以得出100以内任何一个数都可以由以上7个数选择组合得到，
       * 所以对物品数目就不是从0都100遍历，而是0，1，2，4，8，16，32，37遍历，时间大大优化。
       */
      for (let i = 0; i < n; i++) {
          var w = weights[i];
          var v = values[i];
          var num = numbers[i];
          for (let j = 1; ; j *= 2) {
              if (num >= j) {
                  ws[kind] = j * w;
                  vs[kind] = j * v;
                  num -= j;
                  kind++;
              } else {
                  ws[kind] = num * w;
                  vs[kind] = num * v;
                  kind++;
                  break;
              }
          }
      }
      //01背包解法
      var f = new Array(W + 1).fill(0);
      for (let i = 0; i < kind; i++) {
          for (let j = W; j >= ws[i]; j--) {
              f[j] = Math.max(f[j], f[j - ws[i]] + vs[i]);
          }
      }
      return f[W];
  }
  
  var b = mKnapsack([2,3,1 ],[2,3,4],[1,4,1],6)
  console.log(b) //9

进阶背包问题

混合背包问题

不同的物品选择不同的背包即可

二维费用背包问题

问题描述

二维费用的背包问题是指：对于每件物品，具有两种不同的费用，选择这件物品必须同时付出这两种费用。对于每种费用都有一个可付出的最大值（背包容量）。
问怎样选择物品可以得到最大的价值。设第 i 件物品所需的两种费用分别为 Ci 和 Di。两种费用可付出的最大值（也即两种背包容量）分别为 V 和 U。物品的价值为 Wi。

问题分析

费用加了一维，只需状态也加一维即可。设 F[i, v, u] 表示前 i 件物品付出两种费用分别为 v 和 u 时可获得的最大价值。状态转移方程就是：

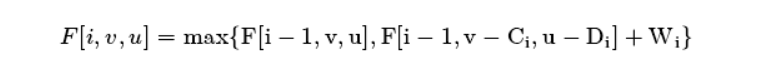
Fate

题目

最近 xhd 正在玩一款叫做 FATE 的游戏，为了得到极品装备，xhd 在不停的杀怪做任务。久而久之 xhd 开始对杀怪产生的厌恶感，但又不得不通过杀怪来升完这最后一级。现在的问题是，xhd 升掉最后一级还需 n 的经验值，xhd 还留有 m 的忍耐度，每杀一个怪 xhd 会得到相应的经验，并减掉相应的忍耐度。当忍耐度降到 0 或者 0 以下时，xhd 就不会玩这游戏。xhd 还说了他最多只杀 s 只怪。请问他能升掉这最后一级吗？
输入数据有多组：
- 对于每组数据第一行输入 n，m，v，s(0 < n,m,v,s < 100) 四个正整数。分别表示还需的经验值，保留的忍耐度，怪的种数和最多的杀怪数。
- 接下来输入 v 行数据。每行数据输入两个正整数 a，b(0 < a,b < 20)；分别表示杀掉一只这种怪 xhd 会得到的经验值和会减掉的忍耐度。(每种怪都有无数个)

输出升完这级还能保留的最大忍耐度，如果无法升完这级输出 -1。

输入：
10 10 1 10
1 1
10 10 1 9
1 1
9 10 2 10
1 1
2 2
输出
0
-1
1
分析
1.还需要10点经验，仍有10点忍耐，只有1种，可以杀10只怪，杀完10只怪，刚刚10点经验，消耗10点忍耐，升级，剩余0忍耐
2.少了一只怪，无法升级
3.杀4只两经验怪+一只1经验怪，剩余1点忍耐

分析

状态：经验
费用：杀怪数和忍耐度
二维费用完全背包问题，参考同一行，对比上一行
状态转移方程：dp[i][k][p]=Math.max(dp[i-1][k][p],dp[i-1][k-1][p-cost[i][1]])+cost[i][0]

初始化分析：要初始化三维比较困难，针对

var fate = function(exe,patience,costs,kill){

  // dp代表的是可以获得的经验
  const dp = new Array(costs.length)
  // 三维数组的初始化，只需要二维
  dp[-1] = []
  for (let i = 0; i < costs.length; i++) {
    dp[i] = []
    dp[i][-1] = new Array(kill).fill(0)
    for (let k = 0; k <= kill; k++) {
      dp[i][k] = new Array(patience+1).fill(0)
      dp[-1][k] = new Array(patience+1).fill(0)
    }
  }
  console.log(dp)
  // 可选择怪的种类
  for (let i = 0; i < costs.length; i++) {
    // 杀怪数
    for (let k = 0; k <= kill; k++) {
      // 忍耐度
      for (let p = 0; p <= patience; p++) {
        if(p<costs[i][1]){
          // 忍耐度不够，直接参考上一种怪
          dp[i][k][p] = dp[i-1][k][p]
        }else{
          // 优先选择第i种怪，在p忍耐度，k杀怪数时的最优情况
          const priority = dp[i][k-1][p-costs[i][1]]+costs[i][0]
          dp[i][k][p]=Math.max(dp[i-1][k][p],priority)
        }
      }
    }
  }
  // 判断是否能升级
  return dp[costs.length-1][kill][patience]>=exe
}

let exe = 10, // 所需经验
    patience = 10, // 忍耐度
    costs = [[1,1]], // 每组怪物可获得的经验和消耗的忍耐度
    kill = 10 // 杀怪数
console.log(fate(exe,patience,costs,kill))

w	v	i\j	2	3	4	5	6	7	8	9	10
2	6	0	6	6	6	6	6	6	6	6	6
2	3	1	6	6	9	9	9	9	9	9	9
6	5	2	6	6	9	9	9	9	11	11	14
5	4	3	6	6	9	9	9	10	11	13	14
4	6	4	6	6	9	9	12	12	15	15	15

w	v	i\j	2	3	4	5	6	7	8	9	10
X	X	-1	0	0	0	0	0	0	0	0	0	0
2	6	0	6	6	6	6	6	6	6	6	6
2	3	1	6	6	9	9	9	9	9	9	9
6	5	2	6	6	9	9	9	9	11	11	14
5	4	3	6	6	9	9	9	10	11	13	14
4	6	4	6	6	9	9	12	12	15	15	15

w	v	i\j	2	3	4	5	6	7	8	9	10
2	6	0	6	6	6	6	6	6	6	6	6
2	3	1	6	6	9	9	9	9	9	9	9
6	5	2	6	6	9	9	9	9	11	11	14
5	4	3	6	6	9	9	9	10	11	13	14
4	6	4	6	6	9	9	12	12	15	15	15

w	v	i\j	2	3	4	5	6	7	8	9	10
X	X	-1	0	0	0	0	0	0	0	0	0	0
2	6	0	6	6	6	6	6	6	6	6	6
2	3	1	6	6	9	9	9	9	9	9	9
6	5	2	6	6	9	9	9	9	11	11	14
5	4	3	6	6	9	9	9	10	11	13	14
4	6	4	6	6	9	9	12	12	15	15	15

w	v	i\j	2	3	4	5	6	7	8	9	10
2	6	0	6	6	6	6	6	6	6	6	6
2	3	1	6	6	9	9	9	9	9	9	9
6	5	2	6	6	9	9	9	9	11	11	14
5	4	3	6	6	9	9	9	10	11	13	14
4	6	4	6	6	9	9	12	12	15	15	15

w	v	i\j	2	3	4	5	6	7	8	9	10
X	X	-1	0	0	0	0	0	0	0	0	0	0
2	6	0	6	6	6	6	6	6	6	6	6
2	3	1	6	6	9	9	9	9	9	9	9
6	5	2	6	6	9	9	9	9	11	11	14
5	4	3	6	6	9	9	9	10	11	13	14
4	6	4	6	6	9	9	12	12	15	15	15