代码随想录

基本思路

当我们知道一个子串不匹配的时候, 我们已经遍历了前面的字符了, 能不能利用上这些信息, 来避免暴力算法中的重复 match 的步骤呢?

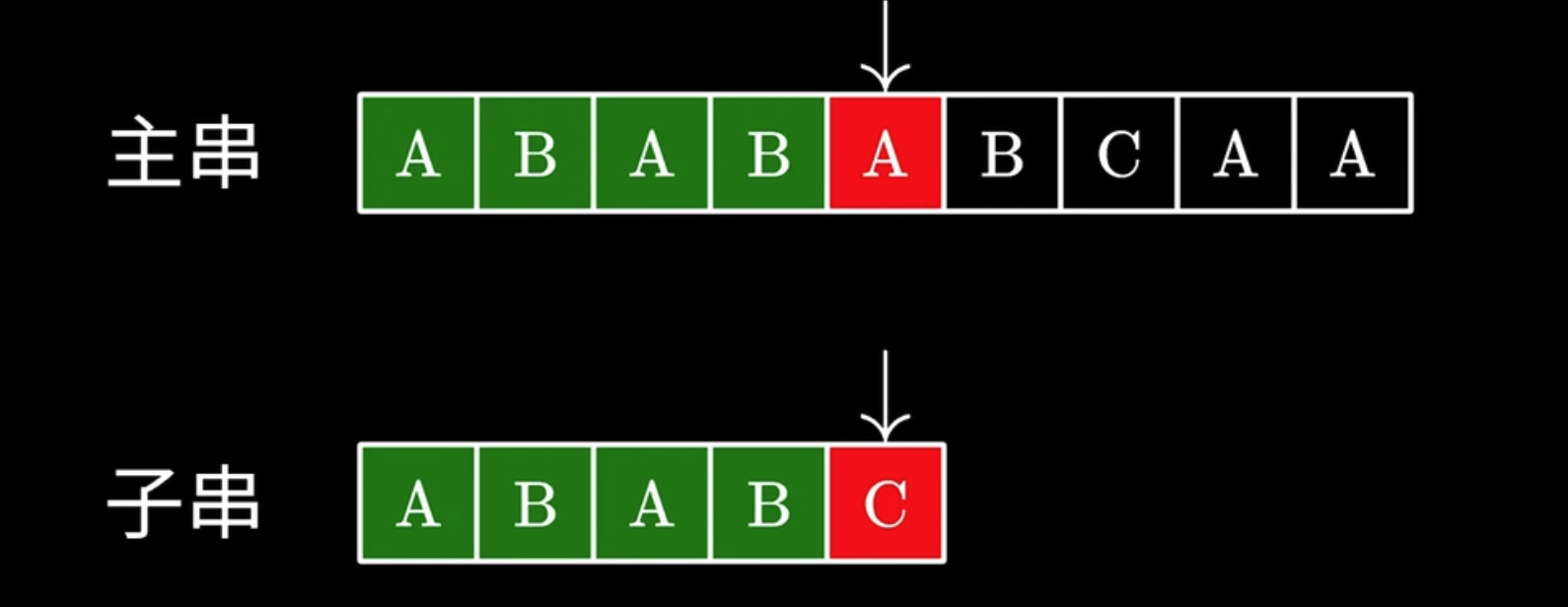
子串在部分代码中又称为模式串

跳过

为什么可以跳过

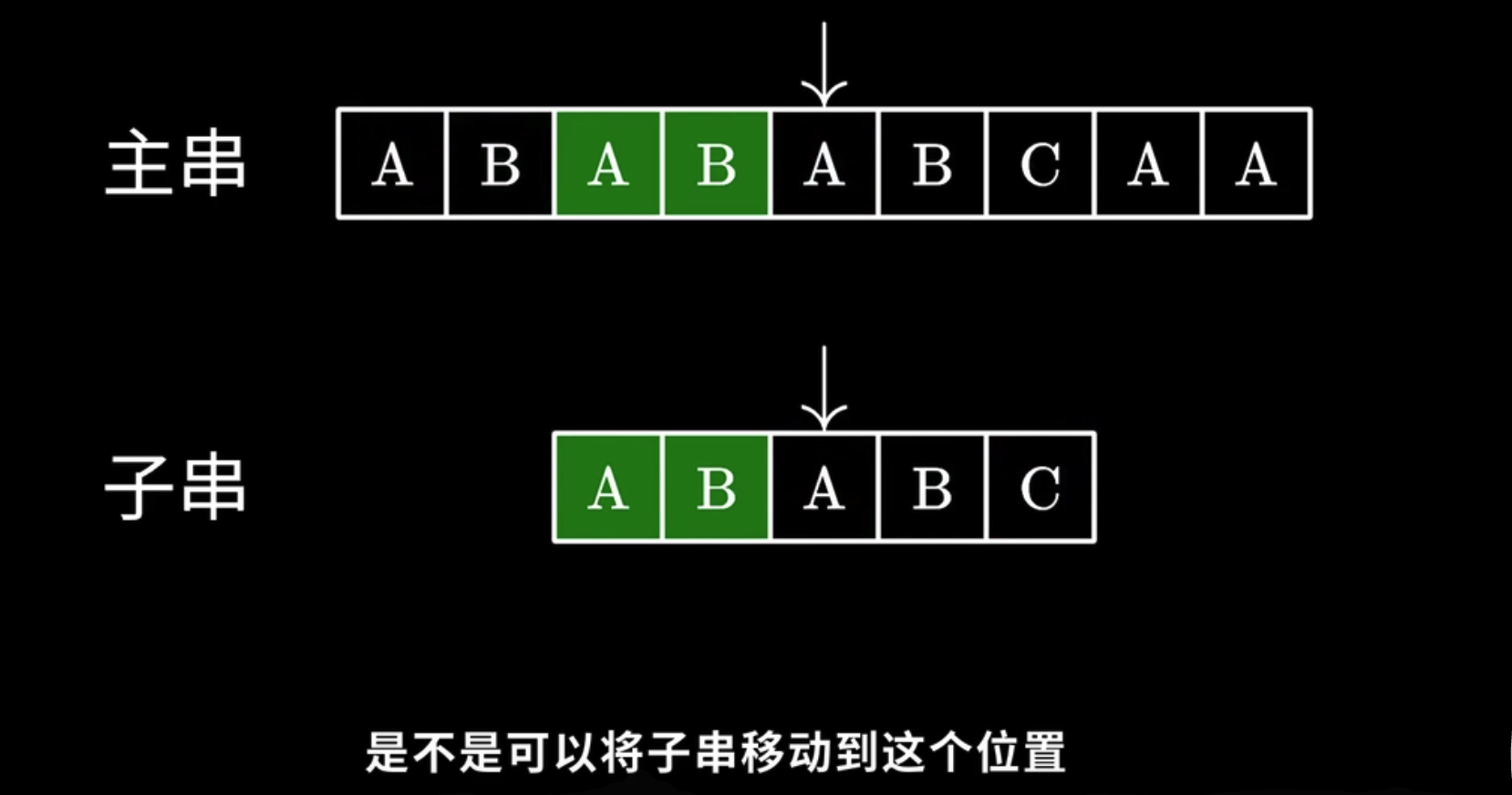
关键是要怎么知道需要跳过多少个字符, 继续进行匹配? 让子串的前缀去匹配主串的后缀

• 对于已经匹配上的 abab 这个子串而言, 它的最长相同前后缀是 ab
• 所以, 我可以让子串的前缀匹配上主串的后缀, 这里要思考的就是为啥可以跳过主串的前缀?
  • 因为原本的是匹配的, 挪一位还是有可能比配上或者匹配不上呀
  • 就比入这里, 只挪一位的话是肯定对不上, 因为是 abab 的形式
  • 但是如果是 aaaa 的话, 前缀和后缀都是 4, 所以 只要 next 数据这里的是 2 就可以直接跳过 2 位没有问题

跳过的收益: 不需要回退主串的指针, 只需要便利一次主串

怎么跳过

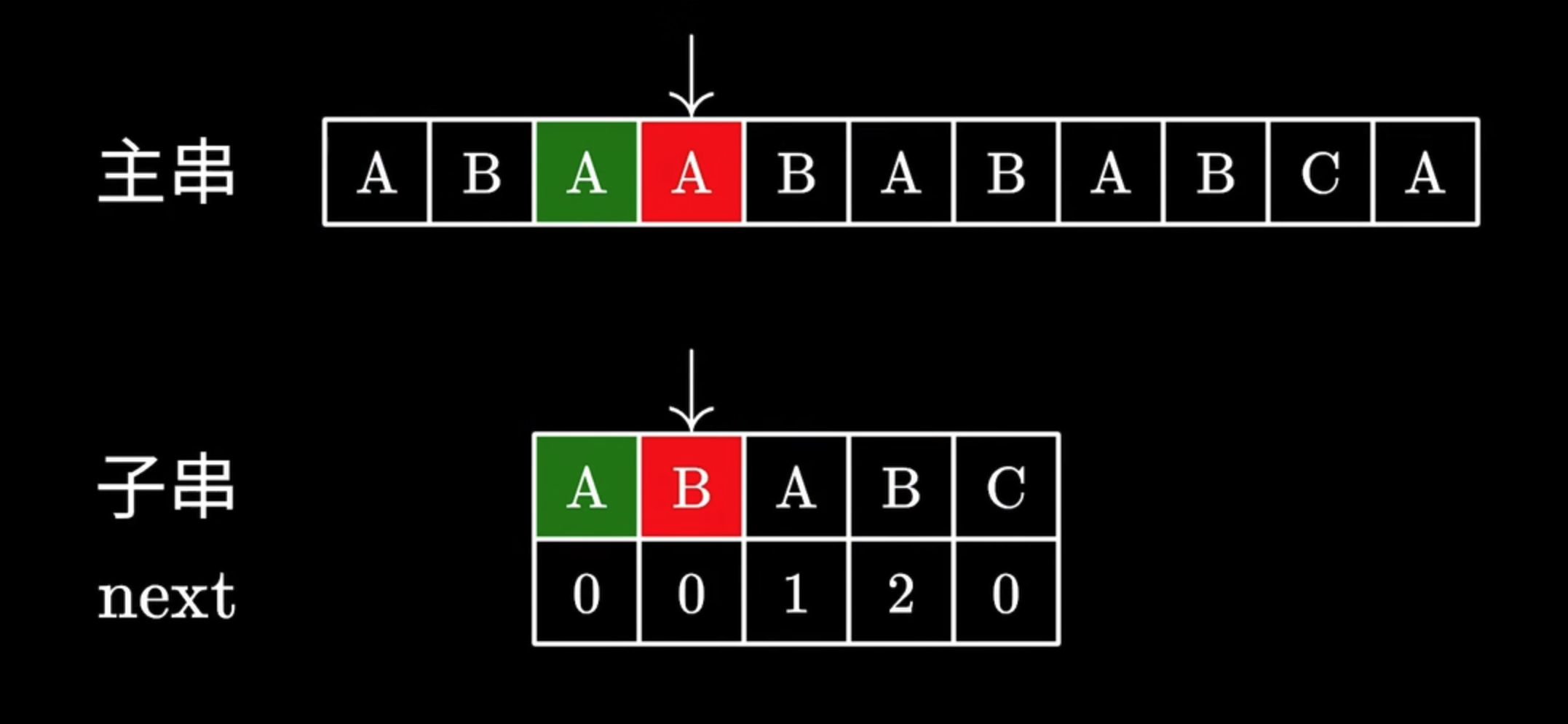
首先, 主串的指针 i 是不动的, 只需要在子串的合适位置重新开始匹配就可以了, 这个位置就是 next[j - 1]

1. 到了 j 匹配出错了, 说明前面的 [0, j - 1] 这个子串是可以匹配上的
2. 对于 [0, j - 1] 这个子串来说, 用这个子串的前缀, 去匹配主串中该子串的后缀
3. 需要重新开始匹配的位置就是 next[j - 1]

伪代码

Next 数组的生成

基本原理

本质就是最长公共前后缀

next[i] 为 [0, i] 的子串的最长公共前后缀

1. 但是不能为字符本身
   1. 因为直接跳过整个子串就没有意义了, 所以第一位 next 为 0
   2. 而且 next[j - 1] 也不可能读取到子串的最后一位, 是不是最后一位就没有意义呢?

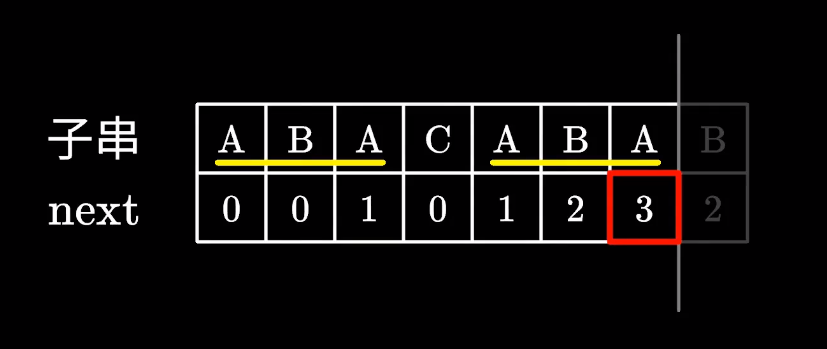
后缀的读写顺序也是从左到右的, 所以后缀是 CABA, 与前缀的 ABAC 并不相等

递推求解 Next 数组

假如下一个字符相同, 只需要在之前的基础上 + 1 即可

如下图, 对于前一个子串 ABACAB 已经匹配上了 AB 前缀和 AB 后缀, 当要求解新增字符的 next[i] 时, 只需要判断在后缀上新增的字符能否匹配上前缀后的那个字符即可, 如果可以匹配上, next[i] = next[i -1] + 1 即可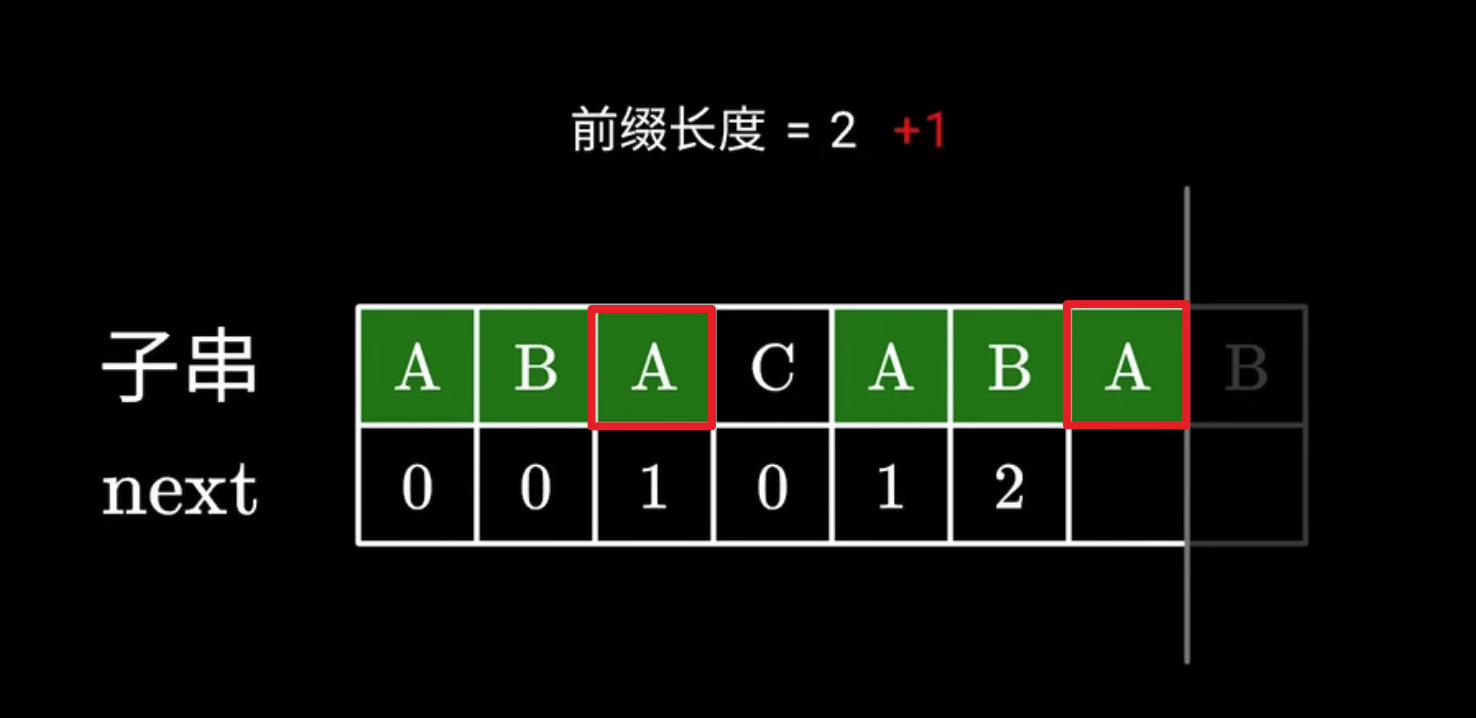

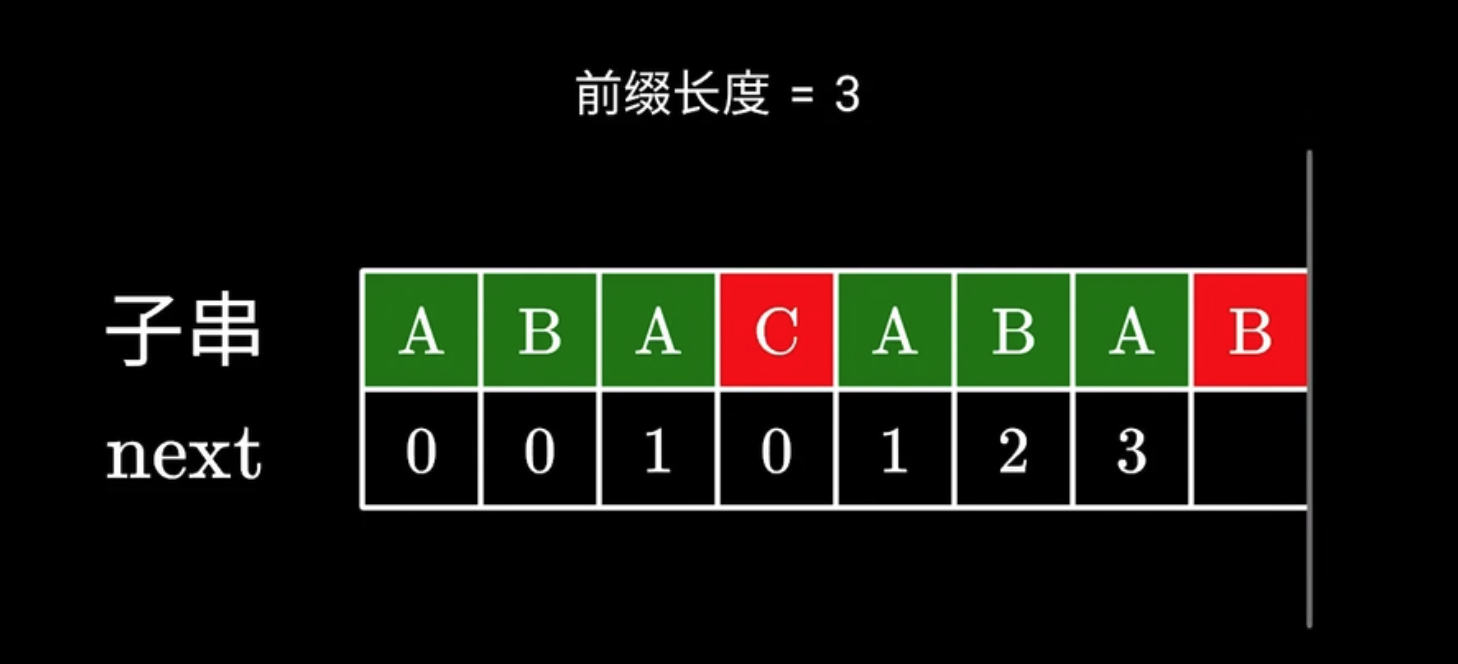
当下一个字符不同的时候, 可以理解为 ABAC 这个主串与 ABAB 这个子串匹配不上, 这里可以套用跳过的思路, 利用已经匹配上的 ABA 这个子串快速进行重新匹配.

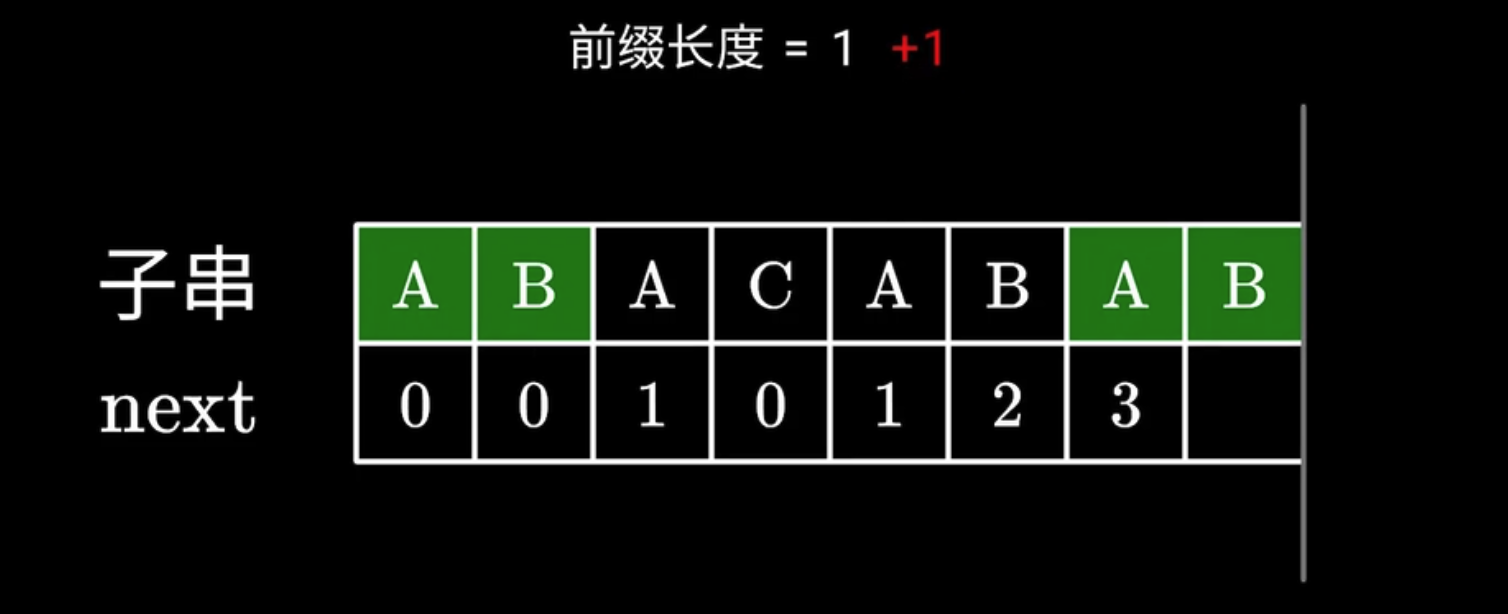
1. 根据之前的经验, 我们要使用后一个 ABA 的后缀, 去匹配前一个 ABA 的前缀, 根据 next 数组, 我们知道有 1 个字符是可以直接匹配上的, 所以我们就可以从下一个位置开始继续寻找公共前后缀了
2. 对于前一个子串而言, 需要把指针挪到 next[i] 的位置, 对于后一个子串而言, 因为是使用后缀进行对齐, 所以需要把指针挪到 next[j - i] 的位置

实现

28. 找出字符串中第一个匹配项的下标

var strStr = function(haystack, needle) {
    const n = haystack.length, m = needle.length;
    if (m === 0) {
        return 0;
    }
    const pi = new Array(m).fill(0);
    // 首位一定为 0, 所以可以直接从 1 开始
    for (let i = 1, j = 0; i < m; i++) {
        while (j > 0 && needle[i] !== needle[j]) {
            j = pi[j - 1];
        }
        if (needle[i] == needle[j]) {
            j++;
        }
        pi[i] = j;
    }
    for (let i = 0, j = 0; i < n; i++) {
        while (j > 0 && haystack[i] != needle[j]) {
            j = pi[j - 1];
        }
        if (haystack[i] == needle[j]) {
            j++;
        }
        if (j === m) {
            return i - m + 1;
        }
    }
    return -1;
};

console.log(strStr('abababcaa', 'ababc'));
console.log(strStr('sadbutsad', 'sad'));

增量算法

一边读入字符串进行匹配, 一边求解当前读入位的 next 数组