!pointer
双指针
这几道题感觉没有啥模板, 就是要根据题意活用双指针
同向双指针
611. 有效三角形的个数: 同向多指针, 三数不等式, 寻找得是区间, 而不是排除. 同样是通过排序, 降低一层循环
他们的共同点, 其实是: 排序 + 子数组, 不要求有序, 不是子串
对撞指针 / 头尾指针
可以用来做反转, reverse
用于缩小搜索范围, 用于排序过的数组, 感觉和前缀和那个有点模糊不清, 需要一个专题处理一下
| File | difficulty | etags |
|---|---|---|
| 9. 回文数 | easy | |
| 633. 平方数之和 | medium | |
| 167. 两数之和 II - 输入有序数组 | medium | |
| 18. 四数之和 | medium | |
| 345. 反转字符串中的元音字母 | easy | |
| 680. 验证回文串 II | easy | |
| 15. 三数之和 | medium | |
| 16. 最接近的三数之和 | medium | |
| 27. 移除元素 | easy | |
| 653. 两数之和 IV - 输入二叉搜索树 | easy | |
| 977. 有序数组的平方 | easy |
哈希表:
快慢指针
快慢指针算法是一种常见的算法技巧,通常用于解决链表相关问题。该算法利用两个指针,在链表上同时移动,但每次移动的步长不同,以达到特定的目的
从这个定义来看, 严格意义上的快慢指针不包含数组原地删除那一块逻辑, 但是官解上都说了是快慢指针, 所以就放在一起吧
处理链表
特定节点
让两个指针拥有固定的间距, 从而达到目的
寻找链表的中间节点:使用快慢指针,快指针每次移动两步,慢指针每次移动一步,当快指针到达链表尾部时,慢指针正好指向链表的中间节点。寻找其他特定节点, 只需要通过快指针和慢指针
链表的倒数第 K 个节点:使用快慢指针,让快指针先移动 K 步,然后快慢指针同时移动,当快指针到达链表尾部时,慢指针指向的节点即为倒数第 K 个节点。
处理回文链表
判断链表的回文结构:使用快慢指针和反转链表的技巧,可以判断链表是否是回文结构。快指针每次移动两步,慢指针每次移动一步,当快指针到达链表尾部时,慢指针指向链表的中间节点。然后反转慢指针后面的链表,再使用两个指针从头和中间开始同时遍历比较,如果节点值不相等,则链表不是回文结构。
处理环
判断链表是否存在环:
- 使用快慢指针,如果存在环,快指针最终会追上慢指针,可以通过比较两个指针是否相等来判断是否存在环。
- 不存在环的话就会遍历结束
感觉不如哈希表快? 参考 160. 相交链表 的处理, 记录一下, 如果重复了就存在环
但是哈希表不能判断环的长度? 可以的, 记录的时候同时记一下长度就行, 然后重复的时候就是环的长度, 第一个重复的点就是环的起点, 但是这种题目的考点更多还是希望能够使用快慢指针实现
我们可以使用在无向图中找环的一个经典算法:快慢指针来解决本题
判圈算法
Flyod 龟兔算法 快慢指针
| File | difficulty | etags | date-created |
|---|---|---|---|
| 141. 环形链表 | easy | 2023-05-30-Tue, 10:49:46 am | |
| 142. 环形链表 II | medium | 2023-07-30-Sun, 9:28:58 am | |
| 287. 寻找重复数 | medium | 2023-07-30-Sun, 9:13:16 am | |
| 457. Circular Array Loop | medium | 2023-05-31-Wed, 7:55:16 pm | |
| 565. 数组嵌套 | medium | 2023-06-18-Sun, 9:45:38 pm |
原理
对于赛道来说,如果赛道中有环,那么速度快的兔子一定会在某个地点追上乌龟,并且兔子所跑的距离减去乌龟所跑的距离,一定是环长度的整数倍。
假设令龟、兔为指针,并且指向起点位置,兔子每次移动两个节点,乌龟每次移动一个节点。如果两者在起始节点外相遇,则说明有环。如果兔子在走到链表尾部还没有与乌龟相遇,说明无环。
环长度
通过上述算法判断出存在环 C 时,显然龟兔位于同一节点 B,此时,令兔子保持不动,而乌龟不断推进,记录移动距离,等再次相遇时,移动步数即环 C 长度。
环起点
乌龟所跑距离为 S = m + n + aC(C 为环长度),
兔子所跑距离为 2S = m + n + bC(因为兔子速度为乌龟 2 倍)
故得 S = (b - a)C = m + n + aC => (b - 2a)C = m + n, 由此可知,m + n 为环 C 长度整数倍
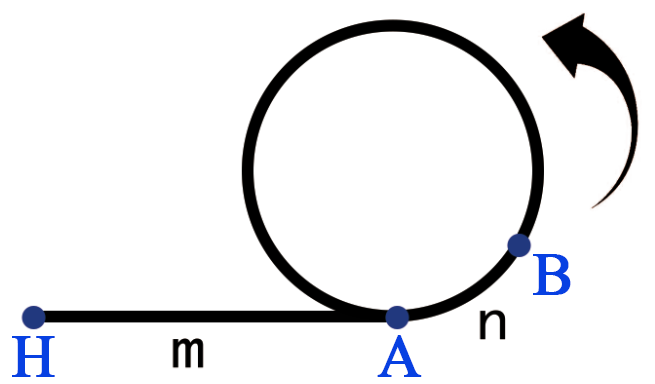
两者相遇之后, 让兔子回到起点 H, 乌龟停留在相遇点 B, 随后, 同时让乌龟与兔子不断推进一步, 兔子移动 m 到达点 A, 距离点 B 还有 n, 乌龟移动 m 也会到达点 A, 再走 n 就饶了 (b-2a) 圈,到达点 B
所以龟兔会在点 A 相遇,之后一直为伴走距离 n 再次到达点 B
实现
function flyodCircle(head) {
let rabbit = head,
tortoise = head;
do {
// 兔子先走,走两步
if (rabbit.next != null) rabbit = rabbit.next;
else return false;
if (rabbit.next != null) rabbit = rabbit.next;
else return false;
tortoise = tortoise.next;
} while (rabbit !== tortoise);
// 出循环,此时龟兔相遇在点B
// 求环长度C
let circleLen = 0;
do {
tortoise = tortoise.next;
circleLen++;
} while (tortoise !== rabbit);
// 求环起点A
tortoise = head;
while (tortoise !== rabbit) {
tortoise = tortoise.next;
rabbit = rabbit.next;
}
// 出循环,此时龟兔相遇在起点A
const start = tortoise;
return { start, circleLen };
}
时间复杂度
如果乌龟走到环起点 P 时,此时显然兔子已经在环内某节点,之后兔子最多走一圈就会与乌龟相遇。假设链表起始节点到环起点距离为 m, 环长度为 n, 故时间复杂度为 O(m + n)
空间复杂度
算法仅需要创建指针 tortoise,rabbit ,环长 circleLen 以及环起点 start 故空间复杂度为 O(1)
Brent 龟兔算法
原理
这是一个倍增算法,让乌龟保持不动,兔子走 2^i 步,看这个过程中龟兔有没有相遇,没有的话,让乌龟的位置变成兔子的位置(如果乌龟位置一直不变,它可能不会进入环中),让兔子走 2^(i+1) 步,看看会不会相遇,如此循环。这个算法也是 O(n) 的,但是它会比 Floyd 表现的更好,且 Floyd 是这个算法最差时的表现。
求环的长度
因为乌龟一直处在兔子更改步长上限时的位置,所以更改步长后,兔子走了几步与乌龟相遇,环的长度就是几步(就是代码中的 count 变量)
求环的起点
Floyd 判圈算法利用了乌龟和兔子的距离是环长整数倍的性质来求出起点,所以可以让乌龟回到起点,兔子回到距离起点 C(C 指环的长度)处,然后接下来的步骤和 Floyd 一样。
实现
function breantCycle(head) {
let rabbit = (tortoise = head);
let stride = 2,
count = 0;
do {
while (count <= stride) {
if (rabbit !== tortise) {
rabbit = rabbit.next;
if (rabbit === null) return false;
count++;
} else {
break;
}
}
tortoise = rabbit;
interval *= 2;
count = 0;
} while (rabbit !== tortoise);
// 出循环,龟兔相遇
const circleLen = count;
// 求环起点A
tortoise = rabbit = head;
while (count > 0) {
rabbit = rabbit.next;
count--;
}
while (tortoise !== rabbit) {
tortoise = tortoise.next;
rabbit = rabbit.next;
}
return;
}
原地删除
两题都是要求使用原地算法删除元素, 其实删除和保留是同一个逻辑
快指针跳过要处理元素, 跳过元素就相当于是删除元素, 慢指针永远指向可替换的位置
在慢指针之前的位置都是要保留的元素
其中一个是有序的, 一个是无序的
无序的只能去除指定值, 因为去除重复数相当于是要去除多个指定值了, 所以无序的做不到
- 剑指 Offer 05. 替换空格
- 剑指 Offer 58 - II. 左旋转字符串
- 83. 删除排序链表中的重复元素
- 80. 删除有序数组中的重复项 II
- 82. 删除排序链表中的重复元素 II
- 287. 寻找重复数
- 27. 移除元素
- 26. 删除有序数组中的重复项
- 151. 反转字符串中的单词
283. 移动零 与合并数组好像, 即是原地算法, 但是又和之前的原地标记不同, 这里借用的是双指针, 数组原地删除、 数组原地交换, 数组原地合并, 这几个很类似, 要好好总结一下才行