prefix-sum
前缀和数组与差分数组
什么是前缀和数组
前缀和数组是指对原数组进去前缀和运算得到的新数组。即 presum[i]=nums[0]+..+nusm[i-1]
什么是差分数组
差分数组是指对原数组进行差分运算得到的新数组,即 diffix[i]=nums[i]-nums[i-1]
关系
两种构建通过提前预处理构建新数组,在一些区间操作中可以优化复杂度。
前缀和与差分数组的转换关系如下:
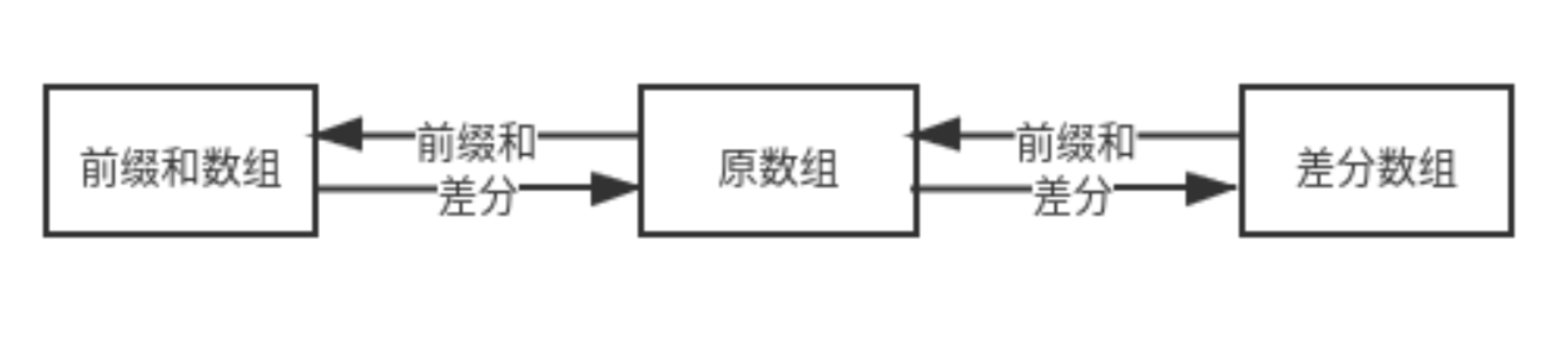
通常来说,假设原数组为 nums,前缀和数组为 prefix,差分数组为 diffix。那么 nums 和 diffix 的长度相等,而 prefix 要多一个元素,插入第一个元素为 0,二维则是左侧和上方多一排元素,这可以方便代码编写
在 js 中, 允许负数索引, 使用 -1 去初始化更好理解, 类似 dummyHead 和 动态规划初始化的思想
通常来说,有这些操作:
- 对原数组求前缀和数组(可以在原数组基础上做)
- 对原数组求差分数组
- 对前缀和数组查询任意区间的和, 即是 子数组和 的相关问题
- 差分数组修改任意区间
- 差分数组求原数组
而前缀和与差分的区别在于:
- 前缀和主要用于原数组不会变化的情况下,频繁查询区间和
- 差分则是用于频繁对原数组某区间元素进行增删的时候
前缀和应用
前缀和与差分都是用在区间操作中的,同样的数据结构还有树状数组,线段树等等。
上面是前缀和与差分的基本运算,实际上还有一些引申,比如前缀和可能不是求和,而是求前缀数组的某个性质,比如说字符种类等等。也可能是异或,乘积运算,而不是和。
- 求最大的平均值: 其实就是子数组长度固定, 然后子数组和最大
除了前缀外,也可能与后缀和同时使用等。
而前缀和通常是求两个 presum,是确定的,暴力就是遍历两遍 O(n^2 ),而常见的优化方式就是用哈希表存储左边的 presum,遍历右边的 presum,优化到线性。
同时,在计数问题中,比如 xx 出现多少次,xx 和 xx 的数量相等这种问题,经常可以把原数组进行变化,如变化为相反数 1 和 -1,或者 0,把计数问题转换为求和问题。
此外,前缀和还经常和同余定理同时使用,同余定理: (presum2-presum1)%k → presum2%k-presum1%k=0 → (presum2%k+k)%k=(presum1%k+k)%k.
差分数组的应用
和前缀和思想非常类似的算法技巧「差分数组」,差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
前缀和与滑动窗口
两者都是解决子数组问题
但是前缀和是 子数组和的各种延伸
滑动窗口
也被归类为 dp ,然后因为可以根据前一个计算后一个, 也是一种动态的, 可以利用滚动思想, 节约空间复杂度
一次性搞定前缀和: Loading Question... - 力扣(LeetCode)
Loading Question... - 力扣(LeetCode)
涉及连续子数组的问题,我们通常有两种思路:一是滑动窗口、二是前缀和。
209. 长度最小的子数组 题解 - 力扣(LeetCode)
因此如果一道题你可以用暴力解决出来,而且题目恰好有连续的限制, 那么滑动窗口和前缀和等技巧就应该被想到。
计算前缀和
开辟新数组
在元数组的基础上
var runningSum = function(nums) {
const n = nums.length;
for (let i = 1; i < n; i++) {
nums[i] += nums[i - 1];
}
return nums;
};
子数组和问题
暴力法
遍历每一个子数组, 然后求和, 其实很多子数组的求和都是重复的, 可以参考动态规划的思路.
通过动态规划优化之后, 我们总结出一种经典场景, 就是前缀和
子数组和等于前缀和的差
对于数组 nums, 定义它的前缀和 s[0] = 0, s[i+1] = sum(nums[0-j])
定义
s[0], 最终 prefixSum 数组的长度为 nums.length + 1, 因为初始化工作比较简单, 就不像动态规划的子序列问题那样定义 i - 1 去处理了, 直接用 dummyHead 思想, 通过哨兵解决
根据这个定义, 有 s[i+1] = s[i] + nums[i]
例如 nums = [1,2,1,2], 对应的前缀和数组为 s = [0, 1, 3, 4, 6]
通过前缀和, 我们可以把子数组的元素和转换成两个前缀的差, 即:
但是这个公式其实也不快的, 还需要两重循环遍历 i 和 j
相关题目
前缀和与哈希表
560. 和为 K 的子数组
结合哈希表, 优化寻找和为 target 的子数组的过程. 可以理解为 1. 两数之和 的升维版本
1248. 统计「优美子数组」
525. 连续数组
二叉树变体: 子路径和即是子数组和
结合树的遍历与回溯, 在每条树的路径上都可以构建一个当前路径的前缀和 Map
注意 index 问题, 包含当前节点的前缀和, 减去前缀和 Node i , 相等于是从当前节点出发, 到 node i 的子节点的路径
437 中只关注 target 从而简化了前缀和的 index 逻辑
更多题目
子数组和的最值问题
最大值、最小值
53. 最大子数组和
1749. 任意子数组和的绝对值的最大值
更多题目
| File | overview |
|---|---|
| 643. 子数组最大平均数 I | 643. 子数组最大平均数 I#solution tips |
| 1413. 逐步求和得到正数的最小值 | 1413. 逐步求和得到正数的最小值#solution tips |
除自身以外的数组问题
1991. 找到数组的中间位置
238. 除自身以外数组的乘积
这里不让用除法, 所以还需要求解后缀和, 如果能用除法就可以从 product 直接等式计算出后缀了
相当于是前缀和 + 后缀和的处理, 反向思维同时分情况讨论
差分数组
差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
比如说,我给你输入一个数组 nums,然后又要求给区间 nums[2..6] 全部加 1,再给 nums[3..9] 全部减 3,再给 nums[0..4] 全部加 2,再给...
一通操作猛如虎,然后问你,最后 nums 数组的值是什么?
常规的思路很容易,你让我给区间 nums[i..j] 加上 val,那我就一个 for 循环给它们都加上呗,还能咋样?这种思路的时间复杂度是 O(N),由于这个场景下对 nums 的修改非常频繁,所以效率会很低下。
这里就需要差分数组的技巧,类似前缀和技巧构造的 preSum 数组,我们先对 nums 数组构造一个 diff 差分数组,diff[i] 就是 nums[i] 和 nums[i-1] 之差
构造差分数组 diff,就可以快速进行区间增减的操作,如果你想对区间 nums[i..j] 的元素全部加 3,那么只需要让 diff[i] += 3,然后再让 diff[j+1] -= 3 即可
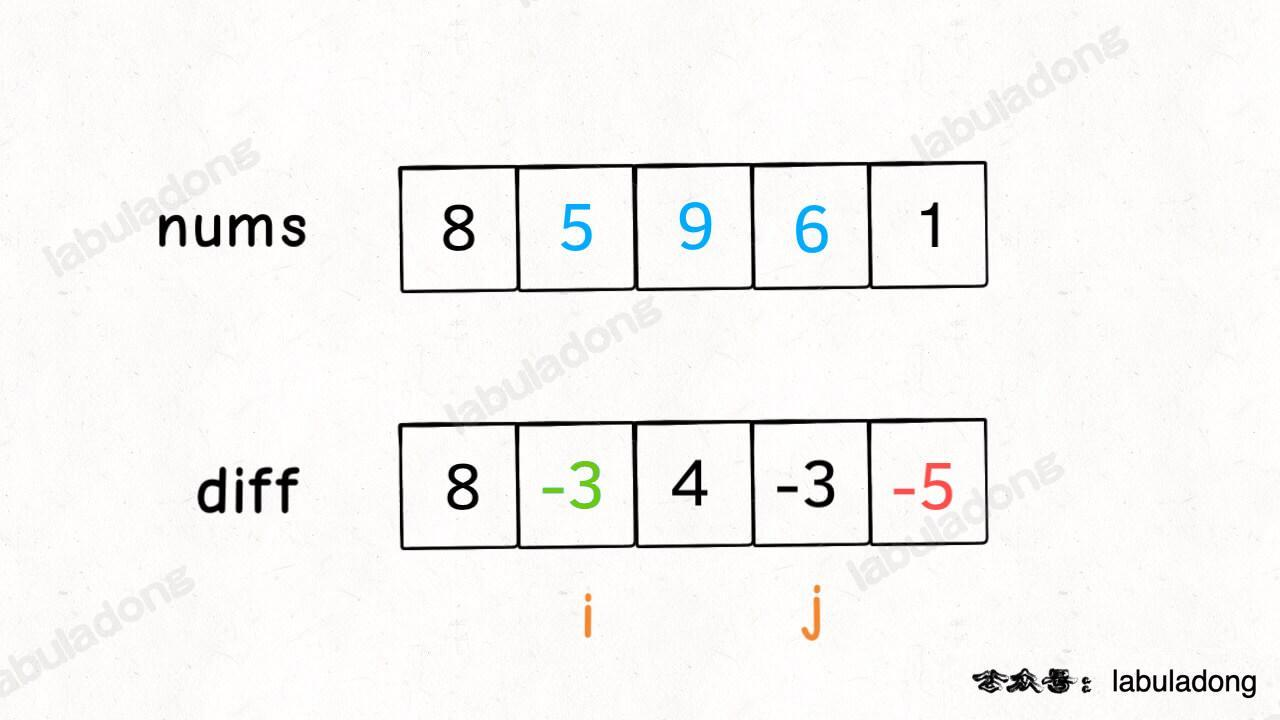
原理很简单,回想 diff 数组反推 nums 数组的过程,diff[i] += 3 意味着给 nums[i] 之后的所有的元素都加了 3,然后 diff[j+1] -= 3 又意味着对于 nums[j+1..] 之后的所有元素再减 3,那综合起来,是不是就是对 nums[i..j] 中的所有元素都加 3 了
// 注意:javascript 代码由 chatGPT🤖 根据我的 java 代码翻译,旨在帮助不同背景的读者理解算法逻辑。
// 本代码还未经过力扣测试,仅供参考,如有疑惑,可以参照我写的 java 代码对比查看。
var Difference = function(nums) {
// 差分数组
this.diff = [];
/* 输入一个初始数组,区间操作将在这个数组上进行 */
if (nums.length > 0) {
this.diff = new Array(nums.length);
// 根据初始数组构造差分数组
this.diff[0] = nums[0];
for (var i = 1; i < nums.length; i++) {
this.diff[i] = nums[i] - nums[i - 1];
}
}
};
/* 给闭区间 [i, j] 增加 val(可以是负数)*/
Difference.prototype.increment = function(i, j, val) {
this.diff[i] += val;
// 当 `j+1 >= diff.length` 时,说明是对 `nums[i]` 及以后的整个数组都进行修改,那么就不需要再给 `diff` 数组减 `val` 了
if (j + 1 < this.diff.length) {
this.diff[j + 1] -= val;
}
};
/* 返回结果数组 */
Difference.prototype.result = function() {
var res = new Array(this.diff.length);
// 根据差分数组构造结果数组
res[0] = this.diff[0];
for (var i = 1; i < this.diff.length; i++) {
res[i] = res[i - 1] + this.diff[i];
}
return res;
};
1109. 航班预订统计
1732. 找到最高海拔
