!graph
概述
图是网络结构的抽象模型。图是一组由边连接的节点(或顶点)。学习图是重要的,因为任何二元关系都可以用图来表示。
任何社交网络,例如 Facebook、Twitter 和 Google plus,都可以用图来表示。
图就是一组节点,以网络的形式互相连接。节点也被称为顶点(vertices)。一对(v,u)就叫做一个边,表示顶点 v 和顶点 u 相连。一个边可能包含权重/成本,显示从顶点 v 到 u 所需的成本
常用小写字母 v 和 u 代表一对相连的顶点,(v,u)代表连接他们的边
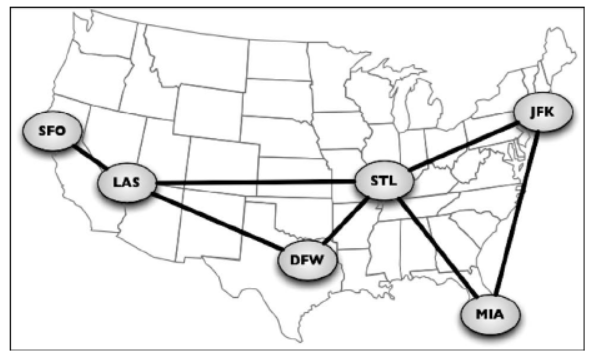
我们还可以使用图来表示道路、航班以及通信状态,如下图所示:
一个图 G = (V, E) 由以下元素组成:
- V:一组顶点
- E:一组边,连接 V 中的顶点
图表示一个图:
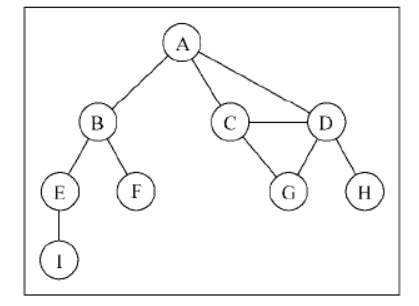
由一条边连接在一起的顶点称为相邻顶点。比如,A 和 B 是相邻的,A 和 D 是相邻的,A 和 C 是相邻的,A 和 E 不是相邻的。
一个顶点的度是其相邻顶点的数量。比如:
- A 和其他三个顶点相连接,因此,A 的度为 3;
- E 和其他两个顶点相连,因此,E 的度为 2。
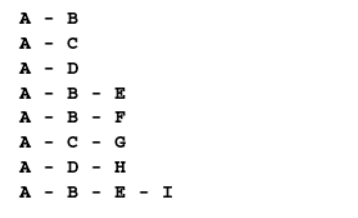
路径是顶点 v1, v2,…,vk 的一个连续序列,其中 vi 和 vi+1 是相邻的。以上一示意图中的图为例,其中包含路径 A B E I 和 A C D G。
简单路径要求不包含重复的顶点。举个例子,A D G 是一条简单路径
环也是一个简单路径,称为简单闭路径,比如 A D C A(最后一个顶点重新回到 A)
如果图中不存在环,则称该图是无环的。如果图中每两个顶点间都存在路径,则该图是连通的
有向图和无向图
图可以是无向的(边没有方向)或是有向的(有向图)。如下图所示,有向图的边有一个方向:
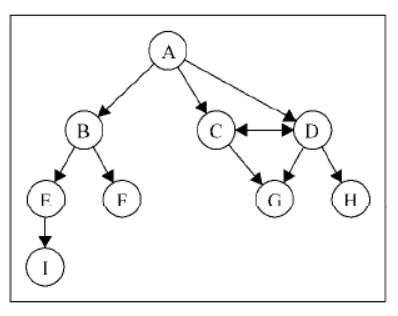
如果图中每两个顶点间在双向上都存在路径,则该图是强连通的。例如,C 和 D 是强连通的,
而 A 和 B 不是强连通的。
有向图中:前溯点和后继点 @@@
predecessor successor
无向图中:前溯点和邻居结点 @@@
predecessor neighbour
图还可以是未加权的(目前为止我们看到的图都是未加权的)或是加权的。如下图所示,加权图的边被赋予了权值:
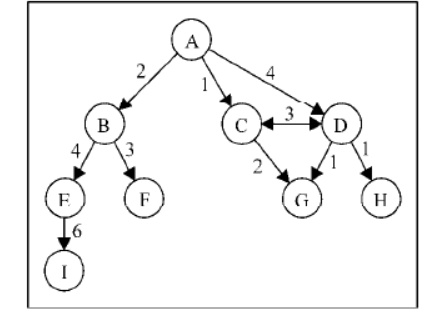
我们可以使用图来解决计算机科学世界中的很多问题,比如搜索图中的一个特定顶点或搜索一条特定边,寻找图中的一条路径(从一个顶点到另一个顶点),寻找两个顶点之间的最短路径,以及环检测。
图的表示
从数据结构的角度来说,我们有多种方式来表示图。在所有的表示法中,不存在绝对正确的方式。图的正确表示法取决于待解决的问题和图的类型。
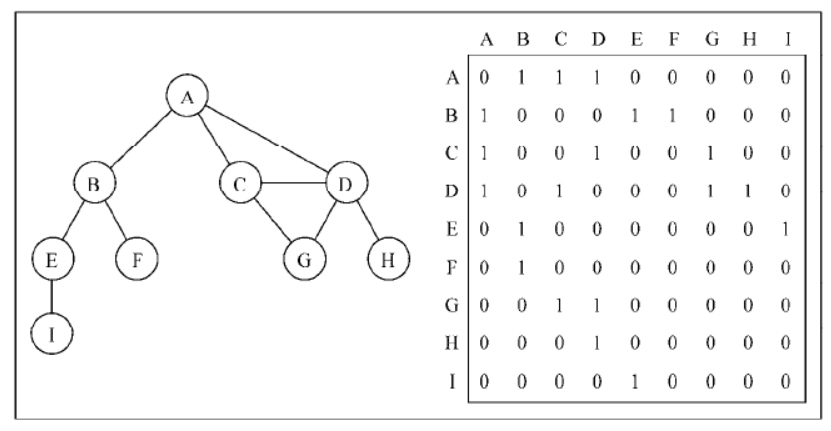
邻接矩阵
图最常见的实现是邻接矩阵。每个节点都和一个整数相关联,该整数将作为数组的索引。我们用一个二维数组来表示顶点之间的连接。如果索引为 i 的节点和索引为 j 的节点相邻,则 array[i][j] === 1,否则array[i][j] === 0,如下图所示:
缺点
不是强连通的图(稀疏图)如果用邻接矩阵来表示,则矩阵中将会有很多 0,这意味着我们浪费了计算机存储空间来表示根本不存在的边。
例如,找给定顶点的相邻顶点,即使该顶点只有一个相邻顶点,我们也不得不迭代一整行
邻接矩阵表示法不够好的另一个理由是,图中顶点的数量可能会改变,而 2 维数组不太灵活。
邻接表
我们也可以使用一种叫作邻接表(adjacency List)的动态数据结构来表示图。邻接表由图中每个顶点的相邻顶点列表所组成。存在好几种方式来表示这种数据结构。我们可以用列表(数组)、链表,甚至是散列表或是字典来表示相邻顶点列表。下面的示意图展示了邻接表数据结构。
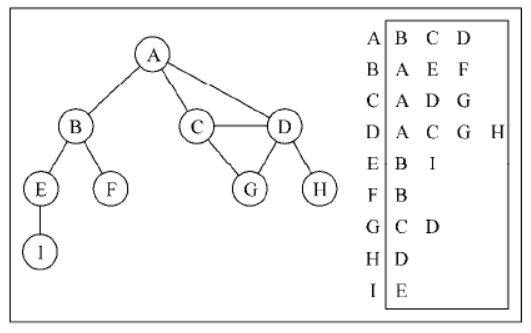
在邻接表中,顶点用键名来表示,边通过键名对应的字典中的元素来表示
对比
尽管邻接表可能对大多数问题来说都是更好的选择,但以上两种表示法都很有用,且它们有着不同的性质
- 要找出顶点 v 和 w 是否相邻,使用邻接矩阵会比较快, 直接访问
matrix[v][w]即可 ???
关联矩阵
我们还可以用关联矩阵来表示图。在关联矩阵中,矩阵的行表示顶点,列表示边。如下图所示,我们使用二维数组来表示两者之间的连通性,如果顶点 v 是边 e 的入射点,则 array[v][e] === 1;否则,array[v][e] === 0。
关联矩阵通常用于边的数量比顶点多的情况下,以节省空间和内存。
图的实现
Graph 类骨架
function Graph() {
const vertices = []; //{1}
const adjList = new Dictionary(); //{2}
}
我们使用一个数组来存储图中所有顶点的名字(行{1}),以及一个字典(在第 7 章中已经实现)来存储邻接表(行{2})。字典将会使用顶点的名字作为键,邻接顶点列表作为值。vertices 数组和 adjList 字典两者都是我们 Graph 类的私有属性。
addVertex()
this.addVertex = function (v) {
vertices.push(v); //{3}
adjList.set(v, []); //{4}
};
这个方法接受顶点 v 作为参数。我们将该顶点添加到顶点列表中(行{3}),并且在邻接表中,设置顶点 v 作为键对应的字典值为一个空数组(行{4})
addEdge()
this.addEdge = function (v, u) {
// 添加从v到u的边
adjList.get(v).push(u); //{5}
// 添加从u到v的边
adjList.get(u).push(v); //{6}
};
这个方法接受两个顶点作为参数。首先,通过将 u 加入到 v 的邻接表中,我们添加了一条自顶点 v 到顶点 u 的边。
如果你想实现一个有向图,则行{5}就足够了。由于本章中大多数的例子都是基于无向图的,我们需要添加一条自 u 向 v 的边(行{6})。
实现有向图和无向图,只有这个方法有区别 @@@
加权图如何实现呢?@@@ 添加边的同时添加权值
this.addEdge = function (v, u, w) {
// 添加从v到u的边
adjList.get(v).push([u, w]); //{5}
// 添加从u到v的边
adjList.get(u).push([v, w]); //{6}
};
toString()
this.toString = function () {
let s = "";
for (let i = 0; i < vertices.length; i++) {
//{10}
s += vertices[i] + " -> ";
// 遍历该顶点的邻接表
const neighbors = adjList.get(vertices[i]); //{11}
for (let j = 0; j < neighbors.length; j++) {
//{12}
s += neighbors[j] + " ";
}
s += "\n"; //{13}
}
return s;
};
我们为邻接表表示法构建了一个字符串。首先,迭代 vertices 数组列表(行{10}),将顶点的名字加入字符串中。接着,取得该顶点的邻接表(行{11}),同样也迭代该邻接表(行{12}),将相邻顶点加入我们的字符串。邻接表迭代完成后,给我们的字符串添加一个换行符(行{13}),这样就可以在控制台看到一个漂亮的输出了。运行如下代码:
var graph = new Graph();
var myVertices = ["A", "B", "C", "D", "E", "F", "G", "H", "I"]; //{7}
for (var i = 0; i < myVertices.length; i++) {
//{8}
graph.addVertex(myVertices[i]);
}
graph.addEdge("A", "B"); //{9}
graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("C", "D");
graph.addEdge("C", "G");
graph.addEdge("D", "G");
graph.addEdge("D", "H");
graph.addEdge("B", "E");
graph.addEdge("B", "F");
graph.addEdge("E", "I");
graph.toString();

Class 实现
class Graph {
vertices = [];
adjList = new Map();
addVertex(vertex) {
this.vertices.push(vertex);
this.adjList.set(vertex, []);
}
addEdge(v, u) {
this.adjList.get(v).push(u)
}
toString() {
let s = "";
for (let i = 0; i < this.vertices.length; i++) {
//{10}
s += this.vertices[i] + " -> ";
// 遍历该顶点的邻接表
const neighbors = this.adjList.get(this.vertices[i]); //{11}
for (let j = 0; j < neighbors.length; j++) {
//{12}
s += neighbors[j] + " ";
}
s += "\n"; //{13}
}
return s;
}
dfs (callback) {
const color = this.initializeColor();
// 直接从 vertices 数组开始递归, 所以不需要起始顶点
for (let i = 0; i < this.vertices.length; i++) {
if (color[this.vertices[i]] === "white") {
this.dfsVisit(this.vertices[i], color, callback);
}
}
}
initializeColor() {
const color = {};
for (let i = 0; i < this.vertices.length; i++) {
color[this.vertices[i]] = "white"; //{1}
}
return color;
}
dfsVisit(v, color, callback) {
color[v] = "grey";
// 第一次遍历顶点时打印
if (callback) callback(v);
const neighbors = this.adjList.get(v);
// 按照字典序排序
neighbors.sort();
for (let i = 0; i < neighbors.length; i++) {
const u = neighbors[i];
if (color[u] === "white") {
this.dfsVisit(u, color, callback);
}
else {
// 每次遍历顶点时打印
if (callback) callback(u);
}
}
color[v] = "black";
}
}
图的遍历
和树数据结构类似,我们可以访问图的所有节点。有两种算法可以对图进行遍历:广度优先搜索(Breadth-First Search,BFS)和深度优先搜索(Depth-First Search,DFS)。
图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径,检查图是否连通,检查图是否含有环等。
图遍历算法的思想是必须追踪每个第一次访问的节点,并且追踪有哪些节点还没有被完全探索。对于两种图遍历算法,都需要明确指出第一个被访问的顶点。
完全探索一个顶点要求我们查看该顶点的每一条边。对于每一条边所连接的没有被访问过的顶点,将其标注为被发现的,并将其加进待访问顶点列表中。
为了保证算法的效率,务必访问每个顶点至多两次。连通图中每条边和顶点都会被访问到。
广度优先搜索算法和深度优先搜索算法基本上是相同的,只有一点不同,那就是待访问顶点列表的数据结构
| 算 法 | 数据结构 | 描 述 |
|---|---|---|
| 广度优先搜索 | 队列 | 通过将顶点存入队列中,最先入队列的顶点先被探索 |
| 深度优先搜索 | 栈 | 通过将顶点存入栈中,顶点是沿着路径被探索的,存在新的相邻顶点就去访问 |
当要标注已经访问过的顶点时,我们用三种颜色来反映它们的状态。
- 白色:表示该顶点还没有被访问。
- 灰色:表示该顶点被访问过,但并未被探索过。
- 黑色:表示该顶点被访问过且被完全探索过。
这就是之前提到的务必访问每个顶点最多两次的原因。
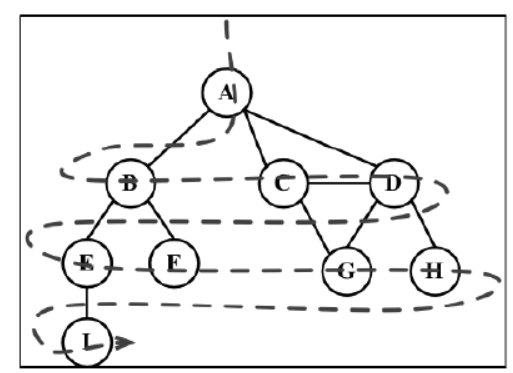
广度优先搜索
广度优先搜索算法会从指定的第一个顶点开始遍历图,先访问其所有的相邻点,就像一次访问图的一层。换句话说,就是先宽后深地访问顶点,如下图所示:
给定源顶点是在特定情况下使用 BFS 算法的要求,如求解最短路径。但如果只是要遍历整个图而不关注最短路径,那么 BFS 可以从任意一个顶点开始,最终都能遍历到所有的节点。
求解最短路径, 正是 BFS 最最常见的场景
常用的场景
常用的用途
以下是从顶点 v 开始的广度优先搜索算法所遵循的步骤:
- 创建一个队列 Q。
- 将 v 标注为被发现的(灰色),并将 v 入队列 Q。
- 如果 Q 非空,则运行以下步骤:
- 将 u 从 Q 中出队列;
- 将标注 u 为被发现的(灰色);
- 将 u 所有未被访问过的邻点(白色)入队列;
- 将 u 标注为已被探索的(黑色)。
this.bfs = function (v, callback) {
const color = initializeColor(),
queue = new Queue();
// 入队作为遍历的起点
queue.enqueue(v);
// 如果队列非空
while (!queue.isEmpty()) {
// 从队列弹出一个顶点
let v = queue.dequeue();
// 获取该顶点的邻接表
neighbors = adjList.get(v);
// 发现了该顶点, 但是还没有完成探索
color[v] = "grey";
// 将所有未被探索的邻居加入队列
for (let i = 0; i < neighbors.length; i++) {
let u = neighbors[i];
if (color[u] === "white") {
// 颜色标记就是为了避免重复将节点推入队列
color[u] = "grey";
queue.enqueue(u);
}
}
// 邻接表访问后, 标记为黑色
color[v] = "black";
if (callback) {
callback(v);
}
}
};
/**
* 广度优先搜索和深度优先搜索都需要标注被访问过的顶点
* 初始化所有的顶点标记为白色
*/
function initializeColor() {
const color = [];
for (let i = 0; i < vertices.length; i++) {
color[vertices[i]] = "white"; //{1}
}
return color;
}
首先,我们声明了一个回调函数(行{16}),它仅仅在浏览器控制台上输出已经被完全探索过的顶点的名字。接着,我们会调用 bfs 方法,给它传递第一个顶点(A——从本章开头声明的 myVertices 数组)和回调函数。当我们执行这段代码时,该算法会在浏览器控制台输出下示的结果:

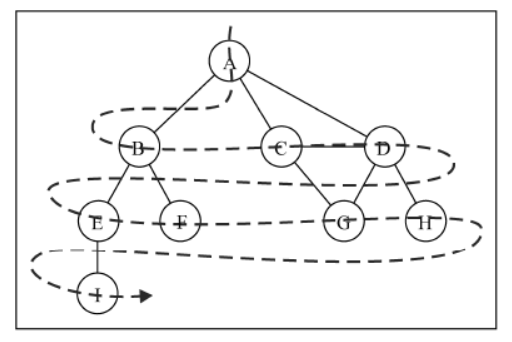
深度优先搜索
深度优先搜索算法将会从第一个指定的顶点开始遍历图,沿着路径直到这条路径最后一个顶点被访问了,接着原路回退并探索下一条路径。换句话说,它是先深度后广度地访问顶点,如下图所示:
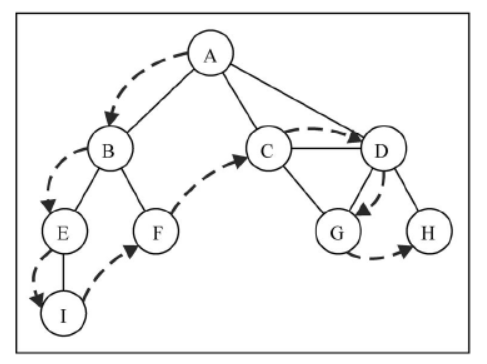
深度优先搜索算法不需要一个源顶点。在深度优先搜索算法中,若图中顶点 v 未访问,则访问该顶点 v。
要访问顶点 v,照如下步骤做:
- 标注 v 为被发现的(灰色)。
- 对于 v 的所有未访问的邻点 w,访问顶点 w,标注 v 为已被探索的(黑色)。
如你所见,深度优先搜索的步骤是递归的,这意味着深度优先搜索算法使用栈来存储函数调用(由递归调用所创建的栈)
让我们来实现一下深度优先算法:
this.dfs = function (callback) {
const color = initializeColor();
// 直接从 vertices 数组开始递归, 所以不需要起始顶点
for (let i = 0; i < vertices.length; i++) {
if (color[vertices[i]] === "white") {
dfsVisit(vertices[i], color, callback);
}
}
};
function dfsVisit(v, color, callback) {
color[v] = "grey";
if (callback) callback(v);
const neighbors = adjList.get(v);
for (let i = 0; i < neighbors.length; i++) {
const u = neighbors[i];
if (color[u] === "white") {
dfsVisit(u, color, callback);
}
}
color[v] = "black";
}
此处的 callback 仅是表意作用,因为很多时候不仅仅需要 v,也需要其他信息,更多的情况下需要在不同的地方增加代码,以深度遍历的形式完成任务,比如拓扑排序
执行过程如下图所示:
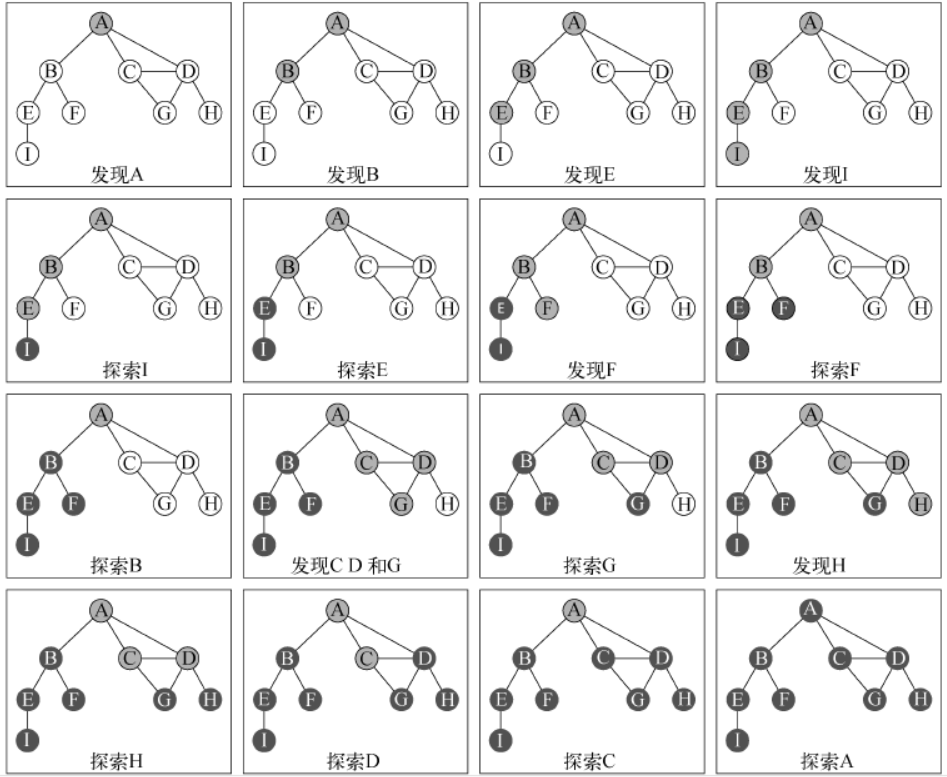
注意
黑白灰三种状态的标记更适合处理复杂的状态, 一般的遍历只需要记住这个节点已经遍历过了就行了, 是类似 boolean 的二元枚举状态
其实只需要邻接表就可以理清一副图了,为什么要需要 vertices 数组呢? 因为不是所有的顶点都是想通的, 不相通的顶点就需要通过 vertices 数组继续完成遍历
如果是有向图,出度邻接表,可能会遗漏出度为 0 的那个顶点(终点),但是仍然可以通过边到达该顶点
常问的图面试问题:
- 实现广度优先搜索和深度优先搜索
- 检查一个图是否为树
- 计算一张图中的边的数量
- 找到两个顶点之间的最短路径
网格类问题
基本概念
我们所熟悉的 DFS(深度优先搜索)问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题,是在一种「网格」结构中进行的。岛屿问题是这类网格 DFS 问题的典型代表。网格结构遍历起来要比二叉树复杂一些,如果没有掌握一定的方法,DFS 代码容易写得冗长繁杂。
本文将以岛屿问题为例,展示网格类问题 DFS 通用思路,以及如何让代码变得简洁。
我们首先明确一下岛屿问题中的网格结构是如何定义的,以方便我们后面的讨论。
网格问题是由 m×n 个小方格组成一个网格,每个小方格与其上下左右四个方格认为是相邻的,要在这样的网格上进行某种搜索。
岛屿问题是一类典型的网格问题。每个格子中的数字可能是 0 或者 1。我们把数字为 0 的格子看成海洋格子,数字为 1 的格子看成陆地格子,这样相邻的陆地格子就连接成一个岛屿。
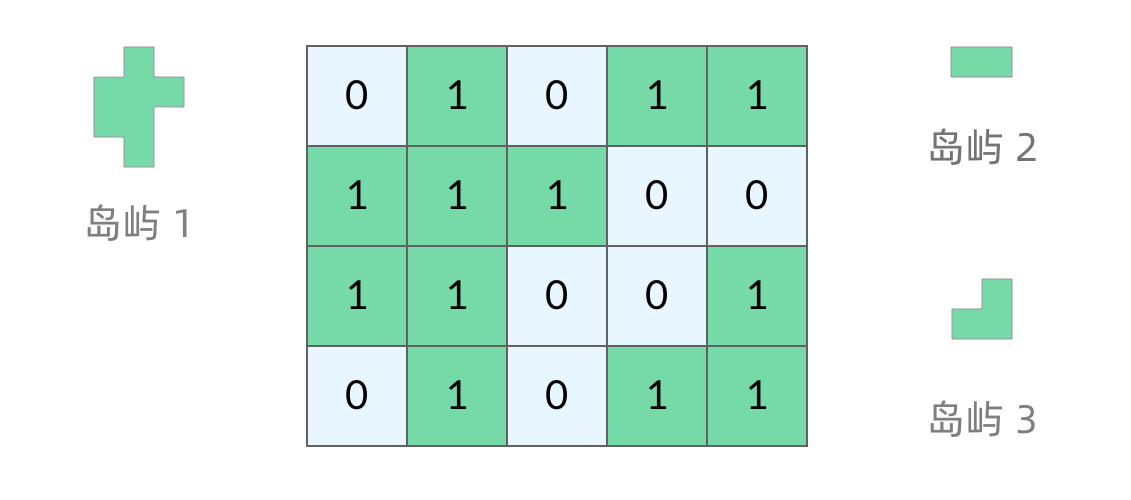
在这样一个设定下,就出现了各种岛屿问题的变种,包括岛屿的数量、面积、周长等。不过这些问题,基本都可以用 DFS 遍历来解决。
DFS 的基本结构
对于网格上的 DFS,我们完全可以参考二叉树的 DFS,写出网格 DFS 的两个要素:
首先,网格结构中的格子有多少相邻结点?答案是上下左右四个。对于格子 (r, c) 来说(r 和 c 分别代表行坐标和列坐标),四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)。换句话说,网格结构是「四叉」的。
其次,网格 DFS 中的 base case 是什么?从二叉树的 base case 对应过来,应该是网格中不需要继续遍历、grid[r][c] 会出现数组下标越界异常的格子,也就是那些超出网格范围的格子。
这一点稍微有些反直觉,坐标竟然可以临时超出网格的范围?这种方法我称为「先污染后治理」—— 甭管当前是在哪个格子,先往四个方向走一步再说,如果发现走出了网格范围再赶紧返回。这跟二叉树的遍历方法是一样的,先递归调用,发现 root == null 再返回。
这样,我们得到了网格 DFS 遍历的框架代码:
void dfs(int[][] grid, int r, int c) {
// 判断 base case
// 如果坐标 (r, c) 超出了网格范围,直接返回
if (!inArea(grid, r, c)) {
return;
}
// 访问上、下、左、右四个相邻结点
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length
&& 0 <= c && c < grid[0].length;
}
如何避免重复遍历
网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于,遍历中可能遇到遍历过的结点。这是因为,网格结构本质上是一个「图」,我们可以把每个格子看成图中的结点,每个结点有向上下左右的四条边。在图中遍历时,自然可能遇到重复遍历结点。
这时候,DFS 可能会不停地「兜圈子」,永远停不下来
如何避免这样的重复遍历呢?答案是标记已经遍历过的格子。以岛屿问题为例,我们需要在所有值为 1 的陆地格子上做 DFS 遍历。每走过一个陆地格子,就把格子的值改为 2,这样当我们遇到 2 的时候,就知道这是遍历过的格子了。也就是说,每个格子可能取三个值:
- 0 —— 海洋格子
- 1 —— 陆地格子(未遍历过)
- 2 —— 陆地格子(已遍历过)
我们在框架代码中加入避免重复遍历的语句:
// 增加填充行, 参考的是 dummyHead 的逻辑
const startRow = Array.from({length: grid[0].length}, () => '0');
const endRow = Array.from({length: grid[0].length}, () => '0');
grid.unshift(startRow);
grid.push(endRow);
function dfs(r, c) {
// if (!inArea(grid, r, c)) return;
if (grid[r][c] !== '1') return;
// 已经遍历过的岛屿标记为 2
grid[r][c] = '2';
// 继续递归四个方向
dfs(r - 1, c);
dfs(r + 1, c);
dfs(r, c + 1);
dfs(r, c - 1);
}
function inArea(grid, r, c) {
// 仔细想一下这个判断其实很重复, 有点没有必要
// 首先 r 只有第一行和最后一行可能越界
// 然后 col 即使越界了也没有关系, 读取到 undefined, bad case 直接结束递归了
// 所以只需要给最开头和最后加上一个填充行就好了
if (r > grid.length -1 || c > grid[0].length - 1) return false;
if (r < 0 || c < 0) return false;
return true;
}
这样,我们就得到了一个岛屿问题、乃至各种网格问题的通用 DFS 遍历方法。以下所讲的几个例题,其实都只需要在 DFS 遍历框架上稍加修改而已。
小贴士: 在一些题解中,可能会把「已遍历过的陆地格子」标记为和海洋格子一样的 0,美其名曰「陆地沉没方法」,即遍历完一个陆地格子就让陆地「沉没」为海洋。这种方法看似很巧妙,但实际上有很大隐患,因为这样我们就无法区分「海洋格子」和「已遍历过的陆地格子」了。如果题目更复杂一点,这很容易出 bug。
岛屿问题
在 LeetCode 中,「岛屿问题」是一个网格系列问题,比如:
| File | difficulty | etags |
|---|---|---|
| 200. 岛屿数量 | medium |
最短路径问题
使用 BFS 寻找最短路径
到目前为止,我们只展示了 BFS 算法的工作原理。我们可以用该算法做更多事情,而不只是输出被访问顶点的顺序。例如,考虑如何来解决下面这个问题。
给定一个图 G 和源顶点 v,找出对每个顶点 u,u 和 v 之间最短路径的距离(以边的数量计)。
对于给定顶点 v,广度优先算法会访问所有与其距离为 1 的顶点,接着是距离为 2 的顶点,以此类推。所以,可以用广度优先算法来解这个问题。我们可以修改 bfs 方法以返回给我们一些信息:
- 从 v 到 u 的距离
d[u]; - 前溯点
pred[u],用来推导出从 v 到其他每个顶点 u 的最短路径。
让我们来看看改进过的广度优先方法的实现:
this.bfs2Graph = function (v) {
const color = initializeColor(),
queue = new Queue(),
d = {}, //{1}
pred = {}; //{2}
queue.enqueue(v);
for (let i = 0; i < vertices.length; i++) {
// 初始化每个顶点到源点的距离为0
d[vertices[i]] = 0
// 前溯点为null
pred[vertices[i]] = null
}
while (!queue.isEmpty()) {
const v = queue.dequeue(),
neighbors = adjList.get(v)
color[v] = 'grey'
for (i = 0; i < neighbors.length; i++) {
var w = neighbors[i]
if (color[w] === 'white') {
color[w] = 'grey'
// 前溯点的距离+1
pred[w] = v //{6}
d[w] = d[v] + 1 //{7}
queue.enqueue(w)
}
}
color[v] = 'black'
}
return { //{8}
distances: d,
predecessors: pred
}
}
初始化每个顶点到源点的距离为 0(行{4}),用 null 来初始化数组 pred。
当我们发现顶点 vertex 的邻点 w 时,则设置 w 的前溯点值为 u(行{7})。我们还通过给 d[u] 加 1 来设置 v 和 w 之间的距离(vertex 是 w 的前溯点,d[vertex] 的值已经更新了)。
方法最后返回了一个包含 d 和 pred 的对象(行{8})。
var shortestPathA = graph.BFS(myVertices[0]);
console.log(shortestPathA);
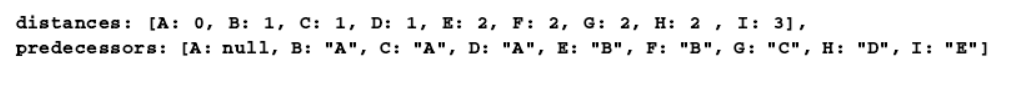
通过前溯点数组,我们可以用下面这段代码来构建从顶点 A 到其他顶点的路径:
this.bfs2Graph = function (v) {
/.../
// 利用前溯点对象打印路径
const start = v,
path = new Stack()
// 刨去起点
const ends = [...vertices]
ends.splice(ends.indexOf(start), 1)
for (let i = 0; i < ends.length; i++) {
let end = ends[i]
while (end !== start) {
path.push(end)
// 变更为前溯点,回溯到start为止
end = pred[end]
}
// 循环结束,栈中保存了该条路径,除了源顶点(A)外的顶点
let s = start
while (!path.isEmpty()) {
// 逐个出栈拼接路径
s += ' - ' + path.pop()
}
console.log(s)
}
console.log(s)
return { //{8}
distances: d,
predecessors: pred
}
}
对于每个其他顶点(除了起点——行{10}),我们会计算顶点 A 到它的路径。我们从顶点数组得到 end(行{11}),然后会创建一个栈来存储路径值(行{12})。
变量 v 被赋值为其前溯点的值,这样我们能够反向追溯这条路径。将变量 v 添加到栈中(行{14})。最后,源顶点也会被添加到栈中,以得到完整路径。
这之后,我们创建了一个 s 字符串,并将源顶点赋值给它(相当于它是最后一个加入栈中的,所以它是第一个被弹出的项 ——行{16})。当栈是非空的,我们就从栈中移出一个项并将其拼接到字符串 s 的后面(行{18})。最后(行{19})在控制台上输出路径。
深入学习最短路径算法
-
本章中的图不是加权图。如果要计算加权图中的最短路径(例如,城市 A 和城市 B 之间的最短路径——GPS 和 Google Maps 中用到的算法),广度优先搜索未必合适。
-
Dijkstra 算法解决了单源最短路径问题。
-
Bellman-Ford 算法解决了边权值为负的单源最短路径问题。
-
A* 搜索算法解决了求仅一对顶点间的最短路径问题,它用经验法则来加速搜索过程。
-
Floyd-Warshall 算法解决了求所有顶点对间的最短路径这一问题。
-
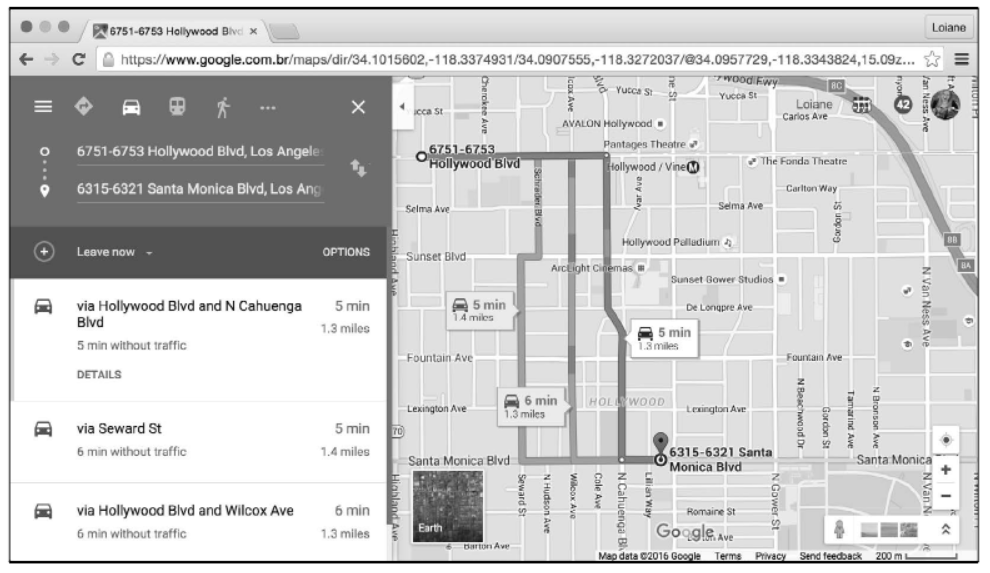
设想你要从街道地图上的 A 点,通过可能的最短路径到达 B 点。举例来说,从洛杉矶的圣莫尼卡大道到好莱坞大道,如下图所示:
-
这种问题在生活中非常常见,我们(特别是生活在大城市的人们)会求助于苹果地图、谷歌地图、Waze 等应用程序。当然,我们也有其他的考虑,如时间或路况,但根本的问题仍然是:A 到 B 的最短路径是什么?
-
我们可以用图来解决这个问题,相应的算法被称为最短路径。本节我们将介绍两种非常著名
的算法,即 Dijkstra 算法和 Floyd-Warshall 算法。
Dijkstra 算法——一到多
- Dijkstra 算法是一种计算从单个源到所有其他顶点的最短路径的贪心算法(你可以在第 11 章了解到更多关于贪心算法的内容),这意味着我们可以用它来计算从图的一个顶点到其余各顶点的最短路径。
算法思想
- 把图中顶点集合 V 分成两组:
- 第一组为已求出最短路径的顶点集合(用 S 表示,初始时 S 中只有一个源点,以后每求得一条最短路径 , 就将加入到集合 S 中,直到全部顶点都加入到 S 中,算法就结束了)
- 第二组为其余未确定最短路径的顶点集合(用 U 表示)
- 按最短路径长度的递增次序依次把第二组的顶点加入 S 中。
- 在加入的过程中,总保持从源点 v 到 S 中各顶点的最短路径长度不大于从源点 v 到 U 中任何顶点的最短路径长度。
- 此外,每个顶点对应一个距离,S 中的顶点的距离就是从 v 到此顶点的最短路径长度,U 中的顶点的距离,是从 v 到此顶点只包括 S 中的顶点为中间顶点的当前最短路径长度。
具体步骤
-
初始时,S 只包含起点 s;U 包含除 s 外的其他顶点,且 U 中顶点的距离为 " 起点 s 到该顶点的距离 "[例如,U 中顶点 v 的距离为 (s,v) 的长度,然后 s 和 v 不相邻,则 v 的距离为∞]。
-
从 U 中选出 " 距离最短的顶点 u",并将顶点 u 加入到 S 中;同时,从 U 中移除顶点 u。
贪心
-
更新 U 中各个顶点到起点 s 的距离。之所以更新 U 中顶点的距离,是由于上一步中确定了 u 是求出最短路径的顶点,从而可以利用 u 来更新其它顶点的距离;例如,(s,v) 的距离可能大于 (s,u)+(u,v) 的距离。
-
重复步骤 (2) 和 (3),直到遍历完所有顶点。
- 当然只要稍加修改,记录一下最短路径时的前溯点,就可以用同样的方法给出最短的路径
实现
-
因为此处使用的是邻接矩阵,所以实现的方式有所不同,通过 visited 数组来区分 S 和 U,本质都是一样的
-
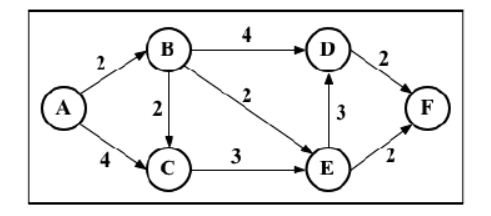
我们来看看如何找到顶点 A 和其余顶点之间的最短路径。但首先,我们需要声明表示上图的邻接矩阵,如下所示:
var graph = [[0, 2, 4, 0, 0, 0], [0, 0, 2, 4, 2, 0], [0, 0, 0, 0, 3, 0], [0, 0, 0, 0, 0, 2], [0, 0, 0, 3, 0, 2], [0, 0, 0, 0, 0, 0]] -
现在,通过下面的代码来看看 Dijkstra 算法是如何工作的:
const dijkstra = function(graph,src) { const length = graph.length, INF = Number. MAX_SAFE_INTEGER // 直接使用Infinity也可以 // 把所有的距离(dist)初始化为无限大,将visited[]初始化为false const dist = new Array(length).fill(INF), // 标记为true的相当于是S visited = new Array(length).fill(false) // 把 源顶点 到 自己的 距离设为0 dist[src] = 0 // 要找出到其余顶点的最短路径 for (let i = 1; i < length; i++) { // 从尚未处理的顶点中选出 距离最近 的顶点,作为局部的最优起点 let v = minDistance(dist, visited) // 把选出的顶点标为visited,以免重复计算 visited[v] = true for (let u = 0; u < length; u++) { if (!visited[u] && graph[v][u] != 0 && dist[v] != INF && dist[v] + graph[v][u] < dist[u]) { // 如果找到更短的路径,则更新最短路径的值 贪心算法 dist[u] = dist[v] + graph[v][u] } } } // 处理完所有顶点后,返回从源顶点到图中其他顶点最短路径的结果 return dist } -
要计算顶点间的 minDistance,就要搜索 dist 数组中的最小值,返回它在数组中的索引
function minDistance(dist, visited) { let min = Number.MAX_SAFE_INTEGER, minIndex = -1 for (let v = 0; v < dist.length; v++) { if (visited[v] == false && dist[v] <= min) { min = dist[v] minIndex = v } } return minIndex } -
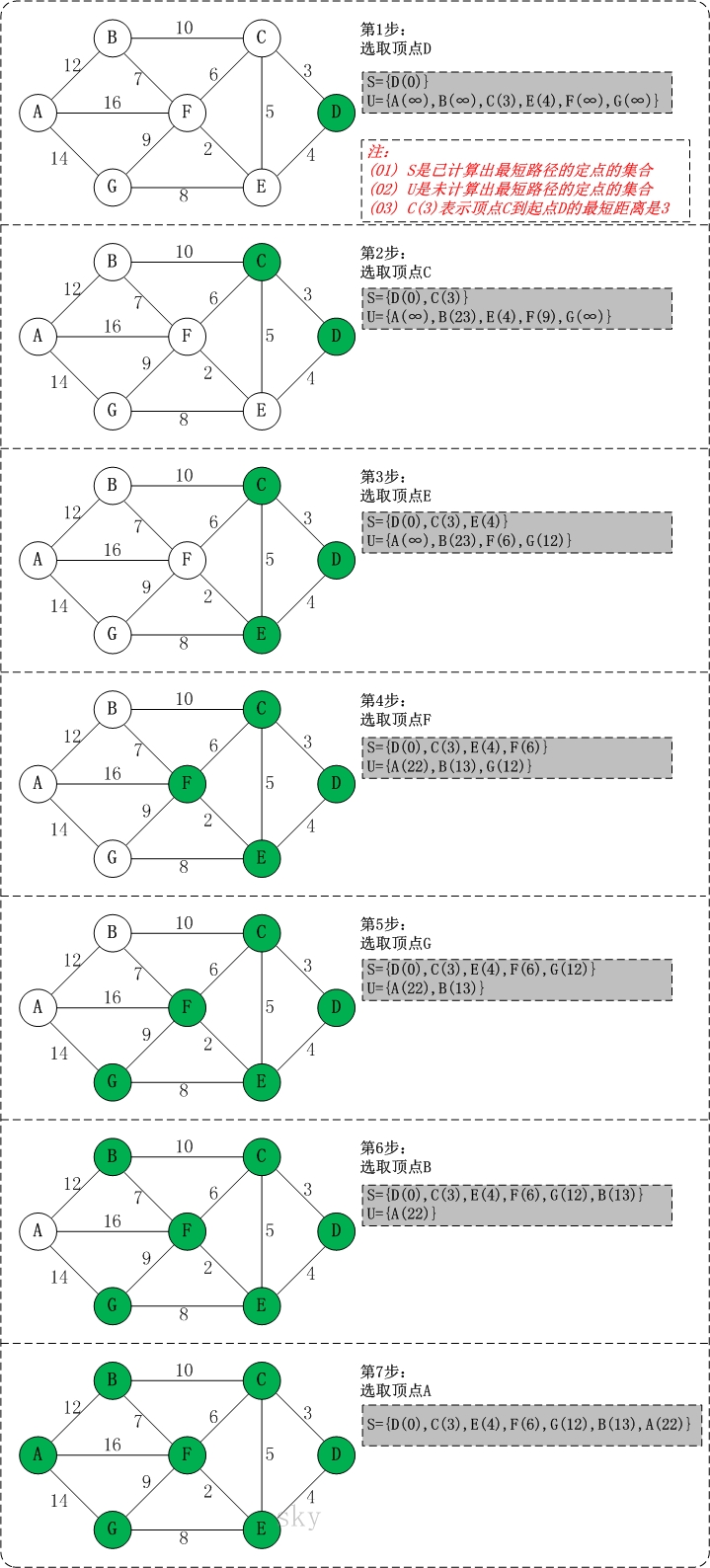
对本节开始的图执行以上算法,会得到如下输出:

参考
- 可以注意到想要渠道 F 点,经过 C 和经过 E 的花费是不同的,一开始先遍历到 C 点,此时到 F 的花费为 9,之后遍历到 E 点,进行了一次更新,因此到达 F 的最短路径是 6
Floyd-Warshall 算法——多到多
-
Floyd-Warshall 算法是一种计算图中所有最短路径的动态规划算法(你可以在第 11 章了解到更
多关于动态规划算法的内容)。通过该算法,我们可以找出从所有源到所有顶点的最短路径。
-
原理:

-
实现如下:
function floydWarshall(graph) { const dist = [], length = graph.length // 首先,把dist数组初始化为每个顶点之间的权值,因为i到j可能的最短距离就是这些顶点间的权值 for (let i = 0; i < length; i++) { //{1} dist[i] = [] for (let j = 0; j < length; j++) { dist[i][j] = graph[i][j]===0?Infinity:graph[i][j] } } // 通过k,得到i途经顶点k,到达j的最短路径 for (let k = 0; k < length; k++) { //{2} for (let i = 0; i < length; i++) { for (let j = 0; j < length; j++) { // 状态转移方程 if (dist[i][k] + dist[k][j] < dist[i][j]) { dist[i][j] = dist[i][k] + dist[k][j] } } } } return dist } var graph = [[0, 2, 4, 0, 0, 0], [0, 0, 2, 4, 2, 0], [0, 0, 0, 0, 3, 0], [0, 0, 0, 0, 0, 2], [0, 0, 0, 3, 0, 2], [0, 0, 0, 0, 0, 0]] console.log(...floydWarshall(graph)) -
对图中每一个顶点执行 Dijkstra 算法,也可以得到相同的结果。
染色问题
1042. 不邻接植花 @@@
题目
-
有 N 个花园,按从 1 到 N 标记。在每个花园中,你打算种下四种花之一。
-
paths[i] = [x, y] 描述了花园 x 到花园 y 的双向路径。
-
另外,没有花园有 3 条以上的路径可以进入或者离开。
-
你需要为每个花园选择一种花,使得通过路径相连的任何两个花园中的花的种类互不相同。
-
以数组形式返回选择的方案作为答案 answer,其中 answer[i] 为在第 (i+1) 个花园中种植的花的种类。花的种类用 1, 2, 3, 4 表示。
-
保证存在答案。
输入:N = 3, paths = [[1,2],[2,3],[3,1]] 输出:[1,2,3]
分析
-
这是一道简单题,限制每个节点的度为 3,同时提供四种颜色,因此不需要回溯
- 存储邻接点信息
- 遍历所有节点,对于每个节点,查看其邻接点颜色,使用不同的颜色染色即可
var gardenNoAdj = function(N, paths) {
const adjList = []
// 初始化邻接表 base 0
for (let i = 0; i < N; i++) {
adjList[i] = []
}
// 初始化路径信息
for (const path of paths) {
// path[0] 到 path[1] 双向路径
// 转化为base0
const [a,b] = [path[0]-1,path[1]-1]
adjList[a].push(b)
adjList[b].push(a)
}
const res =[]
// res base 0
for (let i = 0; i < N; i++) {
const used = new Array(N+1)
const neighbors = adjList[i]
// 记录当前节点的已涂色的邻接点的色彩
for (const n of neighbors) {
if(n<i) used[res[n]] = true
}
// 为当前节点染色
for (let j = 1; j <= 4; j++) {
if(!used[j]){
res[i] = j
break
}
}
}
return res
}
let N = 3, paths = [[1,2],[2,3],[3,1]]
console.log(gardenNoAdj(N,paths))
1000+ms 需要优化
题集
399. 除法求值
题目
-
给出方程式 A / B = k, 其中 A 和 B 均为代表字符串的变量, k 是一个浮点型数字。根据已知方程式求解问题,并返回计算结果。如果结果不存在,则返回 -1.0。
示例 : 给定 a / b = 2.0, b / c = 3.0 问题: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ? 返回 [6.0, 0.5, -1.0, 1.0, -1.0 ] -
输入为:
vector<pair<string, string>> equations,vector<double>& values,vector<pair<string, string>> queries(方程式,方程式结果,问题方程式), 其中equations.size() == values.size(),即方程式的长度与方程式结果长度相等(程式与结果一一对应),并且结果值均为正数。以上为方程式的描述。 返回vector<double>类型。 -
基于上述例子,输入如下:
equations(方程式) = [ ["a", "b"], ["b", "c"] ], values(方程式结果) = [2.0, 3.0], queries(问题方程式) = [ ["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"] ]. -
输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
分析
最小生成树
概念
-
最小生成树(MST)问题是网络设计中常见的问题。想象一下,你的公司有几间办公室,要以最低的成本实现办公室电话线路相互连通,以节省资金,最好的办法是什么?
-
这也可以应用于岛桥问题。设想你要在 n 个岛屿之间建造桥梁,想用最低的成本实现所有岛
屿相互连通。
-
这两个问题都可以用 MST 算法来解决,其中的办公室或者岛屿可以表示为图中的一个顶点,边代表成本。这里我们有一个图的例子,其中较粗的边是一个 MST 的解决方案。
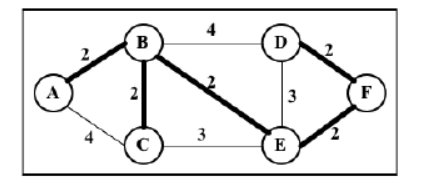
-
本节我们将学习两种主要的求最小生成树的算法:Prim 算法和 Kruskal 算法。
Prim 算法
-
适用于邻接矩阵
-
Prim 算法是一种求解加权无向连通图的 MST 问题的贪心算法。它能找出一个边的子集,使得其构成的树包含图中所有顶点,且边的权值之和最小。
-
现在,通过下面的代码来看看 Prim 算法是如何工作的:
function prim (graph) { const len = graph.length // 首先,把所有顶点(key)初始化为无限大,visited[]初始化为false const key = new Array(len).fill(Infinity), visited = new Array(len).fill(false), pred = [] // 记录前溯点 // 选择第一个key作为第一个顶点 key[0] = 0 // 因为第一个顶点总是MST的根节点,所以pred[0] = -1 pred[0] = -1 // 对所有顶点求MST for (let i = 0; i < len-1; i++) { // 从未处理的顶点集合中选出key值最小的顶点 // 与Dijkstra算法中使用的函数一样,只是名字不同 const v = minKey(key, visited) // 把选出的顶点标为visited,以免重复计算 visited[v] = true for (let u = 0; u < len; u++) { // 如果得到更小的权值,则保存MST路径(parent,行{7})并更新其权值(行{8}) if (graph[v][u] && visited[u] == false && graph[v][u] < key[u]) { pred[u] = v //{7} key[u] = graph[v][u] //{8} } } } // 索引对应的顶点的前溯点 return pred } function minKey(key, visited) { let min = Number.MAX_SAFE_INTEGER, minIndex = -1 for (let v = 0; v < key.length; v++) { if (visited[v] == false && key[v] <= min) { min = key[v] minIndex = v } } return minIndex } var graph = [[0, 2, 4, 0, 0, 0], [2, 0, 2, 4, 2, 0], [4, 2, 0, 0, 3, 0], [0, 4, 0, 0, 3, 2], [0, 2, 3, 3, 0, 2], [0, 0, 0, 2, 2, 0]] console.log(...prim(graph).entries()) -
比较 Prim 算法和 Dijkstra 算法,我们会发现除了行{7}和行{8}之外,两者非常相似。行{7}用 parent 数组保存 MST 的结果。行{8}用 key 数组保存权值最小的边,而在 Dijkstra 算法中,用 dist 数组保存距离。我们可以修改 Dijkstra 算法,加入 parent 数组。这样,就可以在求出距离的同时得到路径。
-
我们会得到如下输出:
Kruskal 算法
-
适用于邻接表和邻接矩阵
-
和 Prim 算法类似,Kruskal 算法也是一种求加权无向连通图的 MST 的贪心算法。
-
现在,通过下面的代码来看看 Kruskal 算法是如何工作的:
/** * kruskal算法 * 遍历所有的边,按权值从小到大排序,每次选取当前权值最小的边,只要不构成回环,则加入生成树 * 邻接矩阵转换成边集数组 * 优点:适合点多边少的情况 * @param graph 邻接矩阵 * @return Array 最小生成树的边集数组 * */ function kruskal(graph) { const edgeArray = getEdgeArr(graph), result = [], // 使用一个数组保存当前顶点的所在的树的终点,即是顶点下标最大的点 // 0表示还没有当前顶点还没有加入任何一颗树 parent = new Array(graph.length).fill(0) let i = 0 // 边数=顶点数-1时就全部联通了 while(result.length<graph.length-1){ const edge = edgeArray[i] // 找到begin顶点的终点,找到end顶点的最终终点 const fx = findParent(parent, edge.begin) const fy = findParent(parent, edge.end) // 合并操作,两个顶点的父亲不同,说明在不同的树,连接不会形成环路 if (fx !== fy) { result.push(edge) // 更新终点 parent[fx] = fy } i++ } console.log(...parent.entries()) return result } var graph = [[0, 2, 4, 0, 0, 0], [2, 0, 2, 4, 2, 0], [4, 2, 0, 0, 3, 0], [0, 4, 0, 0, 3, 2], [0, 2, 3, 3, 0, 2], [0, 0, 0, 2, 2, 0]] console.log(...kruskal(graph).entries()) -
edge 类定义如下:
class Edge { constructor(begin, end, weight) { this.begin = begin this.end = end this.weight = weight } } -
getEdege 定义如下:
/** * 邻接矩阵转邻接表的函数 * @param matrix 邻接矩阵 * @return adjList 邻接表 * */ function getEdgeArr(matrix) { const rows = matrix.length, cols = rows, result = [] for (let i = 0; i < rows; i++) { const row = matrix[i] for(let j = 0 ; j < cols; j++) { if(row[j] !== 0) { result.push(new Edge(i, j, row[j])) } } } result.sort((a, b) => a.weight - b.weight) return result } -
下面是 find 函数的定义,它能防止 MST 出现环路:
/** * 查找连线顶点的尾部下标 * @param parent 判断边与边是否形成环路的数组 * @param v 连线开始的顶点 * @return Number 连线顶点的尾部下标 * */ function findParent(parent, v) { //就是一直循环,直到找到终点 while (parent[v] > 0) v = parent[v] return v }
题集
Leetcode 1135:最低成本联通所有城市
题目
-
想象一下你是个城市基建规划者,地图上有 N 座城市,它们按以 1 到 N 的次序编号。
-
给你一些可连接的选项 conections,其中每个选项
conections[i] = [city1, city2, cost]表示将城市 city1 和城市 city2 连接所要的成本。(连接是双向的,也就是说城市 city1 和城市 city2 相连也同样意味着城市 city2 和城市 city1 相连)。 -
返回使得每对城市间都存在将它们连接在一起的连通路径(可能长度为 1 的)最小成本。该最小成本应该是所用全部连接代价的综合。如果根据已知条件无法完成该项任务,则请你返回 -1。
输入:N = 3, conections = [[1,2,5],[1,3,6],[2,3,1]] 输出:6 解释: 选出任意 2 条边都可以连接所有城市,我们从中选取成本最小的 2 条。
Prim 算法
- 转换成邻接矩阵再使用,没什么必要
Kruskal 算法
-
根据
conections数组获取边成本排序即可function kruskal(N,connections) { // 即使联通所有边都无法联通城市 if(connections.length<N-1) return -1 const edgeArray = getEdgeArr(connections), parent = new Array(N).fill(0) let i = 0, edgeCount = 0,result = 0 while(edgeCount< N - 1){ const edge = edgeArray[i] const fx = findParent(parent, edge[0]) const fy = findParent(parent, edge[1]) if (fx !== fy) { result += edge[2] parent[fx] = fy } i++ edgeCount++ } return result } function getEdgeArr(connections){ return connections.sort((a,b) => a[2]-b[2]) } function findParent(parent, v) { while (parent[v] > 0) v = parent[v] return v } let N = 3, connections = [[1,2,5],[1,3,6],[2,3,1]] console.log(kruskal(N,connections))