graph-dag

DAG

定义和前置条件

定义：将有向图中的顶点以线性方式进行排序。即对于任何连接自顶点u到顶点v的有向边uv，在最后的排序结果中，顶点u总是在顶点v的前面

那么是不是所有的有向图都能够被拓扑排序呢？显然不是。继续考虑上面的例子，如果告诉你在选修计算机科学概论这门课之前需要你先学习机器学习，你是不是会被弄糊涂？在这种情况下，就无法进行拓扑排序，因为它中间存在互相依赖的关系，从而无法确定谁先谁后。在有向图中，这种情况被描述为存在环路

因此，一个有向图能被拓扑排序的充要条件就是它是一个有向无环图 (DAG：Directed Acyclic Graph)。

偏序

假设我们在学习完了算法这门课后，可以选修机器学习或者计算机图形学。这个或者表示，学习机器学习和计算机图形学这两门课之间没有特定的先后顺序。

因此，在我们所有可以选择的课程中，任意两门课程之间的关系要么是确定的 (即拥有先后关系)，要么是不确定的 (即没有先后关系)，绝对不存在互相矛盾的关系 (即环路)

以上就是偏序的意义，抽象而言，有向图中两个顶点之间不存在环路，至于连通与否，是无所谓的。所以，有向无环图必然是满足偏序关系的。

全序

理解了偏序的概念，那么全序就好办了。所谓全序，就是在偏序的基础之上，有向无环图中的任意一对顶点还需要有明确的关系 (反映在图中，就是单向连通的关系，注意不能双向连通，那就成环了)

可见，全序就是偏序的一种特殊情况。回到我们的选课例子中，如果机器学习需要在学习了计算机图形学之后才能学习 (可能学的是图形学领域相关的机器学习算法……)，那么它们之间也就存在了确定的先后顺序，原本的偏序关系就变成了全序关系

实际上，很多地方都存在偏序和全序的概念, 比如对若干互不相等的整数进行排序，最后总是能够得到唯一的排序结果 (从小到大，下同)

但是如果我们以偏序/全序的角度来考虑一下这个再自然不过的问题，可能就会有别的体会了, 那么如何用偏序/全序来解释排序结果的唯一性呢

我们知道不同整数之间的大小关系是确定的，即 1 总是小于 4 的，不会有人说 1 大于或者等于 4 吧。

这就是说，这个序列是满足全序关系的。而对于拥有全序关系的结构 (如拥有不同整数的数组)，在其线性化 (排序) 之后的结果必然是唯一的。

对于排序的算法，我们评价指标之一是看该排序算法是否稳定，即值相同的元素的排序结果是否和出现的顺序一致。比如，我们说快速排序是不稳定的，这是因为最后的快排结果中相同元素的出现顺序和排序前不一致了。如果用偏序的概念可以这样解释这一现象：相同值的元素之间的关系是无法确定的。因此它们在最终的结果中的出现顺序可以是任意的。而对于诸如插入排序这种稳定性排序，它们对于值相同的元素，还有一个潜在的比较方式，即比较它们的出现顺序，出现靠前的元素大于出现后出现的元素。因此通过这一潜在的比较，将偏序关系转换为了全序关系，从而保证了结果的唯一性。

拓展到拓扑排序中，结果具有唯一性的条件也是其所有顶点之间都具有全序关系。如果没有这一层全序关系，那么拓扑排序的结果也就不是唯一的了。在后面会谈到，如果拓扑排序的结果唯一，那么该拓扑排序的结果同时也代表了一条哈密顿路径

拓扑排序模板题: 207. 课程表

207. 课程表

是否存在环

事实上，由于求出一种拓扑排序方法的最优时间复杂度为 O(n+m)，其中 n 和 m 分别是有向图 G 的节点数和边数

而判断图 GGG 是否存在拓扑排序，至少也要对其进行一次完整的遍历，时间复杂度也为 O(n+m)

因此不可能存在一种仅判断图是否存在拓扑排序的方法，它的时间复杂度在渐进意义上严格优于 O(n+m)。

这样一来，我们使用和 210. 课程表 II 完全相同的方法，但无需使用数据结构记录实际的拓扑排序。为了叙述的完整性，下面的两种方法与 210. 课程表 II 的官方题解完全相同，但在「算法」部分后的「优化」部分说明了如何省去对应的数据结构。

实现拓扑排序

深度优先实现拓扑排序

我们可以将深度优先搜索的流程与拓扑排序的求解联系起来，用一个栈来存储所有已经搜索完成的节点。

对于一个节点 u，如果它的所有相邻节点都已经搜索完成，那么在搜索回溯到 u 的时候，u 本身也会变成一个已经搜索完成的节点。这里的「相邻节点」指的是从 u 出发通过一条有向边可以到达的所有节点。

假设我们当前搜索到了节点 u，如果它的所有相邻节点都已经搜索完成，那么这些节点都已经在栈中了，此时我们就可以把 u 入栈。可以发现，如果我们从栈顶往栈底的顺序看，由于 u 处于栈顶的位置，那么 u 出现在所有 u 的相邻节点的前面。因此对于 u 这个节点而言，它是满足拓扑排序的要求的。

这样以来，我们对图进行一遍深度优先搜索。当每个节点进行回溯的时候，我们把该节点放入栈中。最终从栈顶到栈底的序列就是一种拓扑排序。

探索时间实现拓扑排序

对于给定的图 G，我们希望深度优先搜索算法遍历图 G 的所有节点，构建“森林”（有根树的一个集合）以及一组源顶点（根），并输出两个数组：发现时间和完成探索时间。我们可以修改 dfs 方法来返回给我们一些信息：

顶点 u 的发现时间 d[u] (discovery)
当顶点 u 被标注为黑色时，u 的完成探索时间 f[u]

让我们来看看改进了的 DFS 方法的实现：

let time = 0; //{1} 

this.dfs2Time = function () {
  const color = initializeColor(), //{2} 
      d = {},
      f = {}

  for (let i = 0; i < vertices.length; i++) { //{3} 
      f[vertices[i]] = 0;
      d[vertices[i]] = 0;
  }
  for (let i = 0; i < vertices.length; i++) {
      if (color[vertices[i]] === 'white') {
          DFSVisit(vertices[i], color, d, f, p)
      }
  }
  return {           //{4} 
      discovery: d,
      finished: f,
  }
}

function DFSVisit(v, color, d, f, p) {
  console.log('discovered ' + v)
  color[v] = 'grey';
  d[v] = ++time //{5} 
  const neighbors = adjList.get(v)
  for (let i = 0; i < neighbors.length; i++) {
      const u = neighbors[i];
      if (color[u] === 'white') {
          DFSVisit(u, color, d, f, p)
      }
  }
  color[v] = 'black'
  f[v] = ++time;      //{7}  
  console.log('explored ' + v)
}

我们需要一个变量来要追踪发现时间和完成探索时间（行{1}）

当一个顶点第一次被发现时，我们追踪其发现时间（行{5}）。最后，当这个顶点被完全探索后，我们追踪其完成时间（行{7}）。

深度优先算法背后的思想是什么？边是从最近发现的顶点 u 处被向外探索的。只有连接到未发现的顶点的边被探索了。当 u 所有的边都被探索了，该算法回退到 u 被发现的地方去探索其他的边。这个过程持续到我们发现了所有从原始顶点能够触及的顶点。如果还留有任何其他未被发现的顶点，我们对新源顶点重复这个过程。重复该算法，直到图中所有的顶点都被探索了。

对于改进过的深度优先搜索，有两点需要我们注意：

时间（time）变量值的范围只可能在图顶点数量的一倍到两倍之间；
对于所有的顶点 u，d[u]<f[u]（意味着，发现时间的值比完成时间的值小，完成时间意思是所有顶点都已经被探索过了）。

在这两个假设下，我们有如下的规则： $1 \leq d [u] < f [u] \leq 2 | V |$

如果对同一个图再跑一遍新的深度优先搜索方法，对图中每个顶点，我们会得到如下的发现/完成时间：

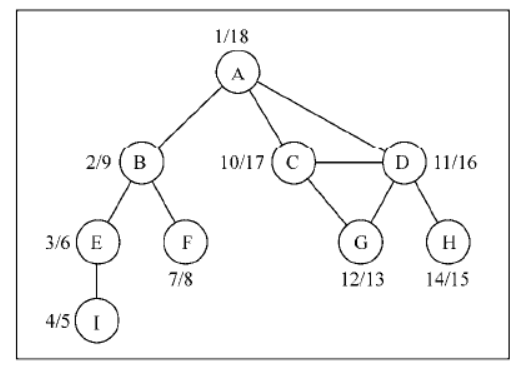
本质：就是深度优先搜索，一遍记录发现和探索完成的时间

现在要做的仅仅是以倒序来排序完成时间数组，这便得出了该图的拓扑排序： B - A - D - C - F - E

注意之前的拓扑排序结果仅是多种可能性之一。如果我们稍微修改一下算法，就会有不同的结果，比如下面这个结果也是众多其他可能性中的一个： A - B - C - D - F - E

Kahn 算法 - 广度优先

具体到拓扑排序，每一次都从图中删除没有前驱的顶点，这里并不需要真正的做删除操作，我们可以设置一个入度数组，每一轮都输出入度为 0 的结点，并移除它、修改它指向的结点的入度（−1 即可），依次得到的结点序列就是拓扑排序的结点序列。如果图中还有结点没有被移除，则说明“不能完成所有课程的学习”。

拓扑排序保证了每个活动（在这题中是“课程”）的所有前驱活动都排在该活动的前面，并且可以完成所有活动。拓扑排序的结果不唯一。拓扑排序还可以用于检测一个有向图是否有环。相关的概念还有 AOV 网，这里就不展开了。

算法流程

在开始排序前，扫描对应的存储空间（使用邻接表），将入度为 0 的结点放入队列。
只要队列非空，就从队首取出入度为 0 的结点，将这个结点输出到结果集中，并且将这个结点的所有邻接结点（它指向的结点）的入度减 1，在减 1 以后，如果这个被减 1 的结点的入度为 0 ，就继续入队。
当队列为空的时候，检查结果集中的顶点个数是否和课程数相等即可。

注意

在代码具体实现的时候，除了保存入度为 0 的队列，我们还需要两个辅助的数据结构：

邻接表：通过结点的索引，我们能够得到这个结点的后继结点；
入度数组：通过结点的索引，我们能够得到指向这个结点的结点个数。

这个两个数据结构在遍历题目给出的邻边以后就可以很方便地得到。

实现

复杂度分析：

初始化入度为0的集合需要遍历整张图，检查每个节点和每条边，因此复杂度为 O(E+V);

然后对该集合进行操作，又需要遍历整张图中的，每条边，复杂度也为 O(E+V);

因此Kahn算法的复杂度即为O(E+V)。

总结

对于基于DFS的算法，加入结果集的条件是：顶点的出度为0。这个条件和Kahn算法中入度为0的顶点集合似乎有着异曲同工之妙，这两种算法的思想犹如一枚硬币的两面。一个是从入度的角度来构造结果集，另一个则是从出度的角度来构造。

实现上的一些不同之处：

Kahn 算法不需要检测图为DAG，如果图为DAG，那么在出度为0的集合为空之后，图中还存在没有被移除的边，这就说明了图中存在环路。
而基于DFS的算法需要首先确定图为DAG，当然也能够做出适当调整，让环路的检测和拓扑排序同时进行，毕竟环路检测也能够在DFS的基础上进行。

二者的复杂度均为O(V+E)

Npm 包依赖分析

出自支付宝一面, 本质上是一样的.