stack
基本
概念
又名“堆栈”,和堆一点关系都没有,是两种完全不同的数据结构
我们都熟悉很有名的撤销(Undo)选项,它几乎存在每个应用程序中。有没有想过它是如何工作的?其思路就是,按照最后的状态排列在先的顺序将工作的先前状态(限于特定数字)存储在内存中。这只用数组是无法实现的,因此堆栈就有了用武之地。
可以把堆栈看作一堆垂直排列的书籍。为了获得位于中间位置的书,你需要拿掉放在它上面的所有书籍。这就是 LIFO(后进先出)方法的工作原理。
栈顶允许操作,栈底不允许操作
这是一个包含三个数据元素(1,2 和 3)的堆栈图像,其中 3 位于顶部,首先把它删除:
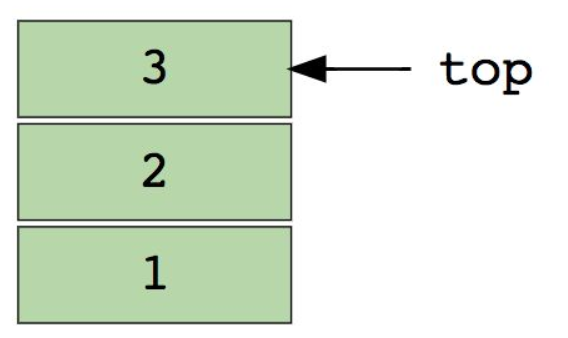
栈的实现
从数据存储的角度看,实现栈有两种方式,一种是以数组做基础,一种是以链表做基础,数组是最简单的实现方式,本文以基础的数组来实现栈。
栈的基本操作包括创建栈、销毁栈、出栈、入栈、获取栈顶元素、获取栈的大小、清空栈。
我们定义以下几个栈的方法:
- push 添加一个元素到栈顶
- pop 弹出栈顶元素
- top/peek 返回栈顶元素
- isEmpty 判断栈是否为空
- size 返回栈里元素的个数
- clear 清空栈
然后我们利用 es6 的 class 的实现以上的方法
class Stack {
constructor() {
this.items = []; // 使用数组存储数据
}
push(item) {
this.items.push(item); // 往栈里压入一个元素
}
pop() {
// 如果不为空
if(!this.isEmpty()) return this.items.pop(); // 把栈顶的元素移除
}
top() {
return this.items[this.items.length - 1]; // 返回栈顶的元素
}
isEmpty() {
return this.items.length === 0; //返回栈是否为空
}
size() {
return this.items.length; // 返回栈的大小
}
clear() {
this.items = []; // 清空栈
}
toString(){
return this.items.reduce(function(str,val){
return str + val
},'')
}
}
上面的方法是否仅仅是对数组做了一层封装?
给你一个数组,你可以通过索引操作任意一个元素,但是给你一个栈,你能操作任意元素么?栈提供的方法只允许你操作栈顶的元素,也就是数组的最后一个元素,这种限制其实提供给我们一种思考问题的方式,这个方式也就是栈的特性,后进先出。
既然栈的底层实现其实就是数组,栈能做的事情,数组一样可以做啊,为什么弄出一个栈来,是不是多此一举?封装是为了更好的利用,站在栈的肩膀上思考问题显然要比站在数组的肩膀上思考问题更方便,后面的练习题你将有所体会。
栈与计算器
难点不是题目本身, 而是需要想到要去用栈高效的处理问题
栈与括号匹配
判断括号是否匹配
()ss()ss(sss(ss)(ss)ss) 合法
()ss()ss(sss(ss)(ss)ss)) 不合法
括号有嵌套关系,也有并列关系,如果我们用数组或者对象的方法也能解决,今天我们试着用栈来解决这个问题。
-
遍历字符串
-
如果是左括号,就压入栈中
-
如果是右括号,判断栈是否为空
- 如果不为空,则把栈顶元素移除 (也就是在栈中存放的左括号),这对括号就抵消了;
- 如果为空,就说明缺少左括号,返回 false
-
循环结束后,看栈的大小是否为 0,如果不为 0,就说明没有成对出现,为 0,就说明全部抵消了。
{
function isDouuble(str) {
const stack = new Stack();
const len = str.length;
for (let i = 0; i < len; i++) {
const item = str[i];
if (str[i] === "(") {
stack.push(item); // 入栈
} else if (item === ")") {
if (stack.isEmpty()) {
return false;
} else {
stack.pop(); // 出栈
}
}
}
return stack.size() === 0;
}
console.log(isDouuble("()ss()ss(sss(ss)(ss)ss)")); // true
console.log(isDouuble("()ss()ss(sss(ss)(ss)ss)(")); // false
console.log(isDouuble("()ss()ss(sss(ss)(ss)ss))")); // false
console.log(isDouuble("()ss()ss(sss(ss)(ss)ss))(")); // false
}
20. 有效的括号
基本应用
| File | difficulty | etags | date-created |
|---|---|---|---|
| 1124. 表现良好的最长时间段 | medium | 2023-08-19-Sat, 3:09:21 pm | |
| 20. 有效的括号 | easy | 2023-05-21-Sun, 6:16:14 pm | |
| 224. 基本计算器 | hard | 2023-05-21-Sun, 5:47:35 pm | |
| 42. 接雨水 | hard | 2023-07-19-Wed, 7:22:20 pm | |
| 445. 两数相加 II | medium | 2023-05-23-Tue, 4:10:35 pm | |
| 496. 下一个更大元素 I | easy | 2023-07-19-Wed, 3:37:09 pm | |
| 503. 下一个更大元素 II | medium | 2023-07-19-Wed, 4:00:07 pm | |
| 591. 标签验证器 | hard | 2023-05-21-Sun, 6:43:37 pm | |
| 636. 函数的独占时间 | medium | 2023-05-21-Sun, 6:24:26 pm | |
| 654. 最大二叉树 | medium | 2023-06-03-Sat, 10:12:52 pm | |
| 682. 棒球比赛 | easy | 2023-05-20-Sat, 9:34:41 pm | |
| 71. 简化路径 | medium | 2023-05-20-Sat, 9:42:39 pm | |
| 739. 每日温度 | medium | 2023-07-19-Wed, 3:09:35 pm | |
| 84. 柱状图中最大的矩形 | hard | 2023-07-20-Thu, 10:17:30 am |
844. 比较含退格的字符串
实现一个 Min 方法的栈
双栈
实现一个栈,除了常见的 push,pop 方法以外,提供一个 min 方法,返回栈里最小的元素,且时间复杂度为
可以利用两个栈来实现,一个栈用来存储数据,一个栈用来存储栈里最小的数据;利用编程中分而治之的思想,就是分开想分开处理
- 定义两个栈,dataStack 和 minStack;
- 对于 dataStack 栈来说,正常的 psuh,pop 实现就好;
- 对于 minStatck 栈来说,它是要存储栈里最小的值,所以当 minStack 为空的时候,那么 push 进来的数据就是最小的;如果不为空,此时 minStack 栈顶的元素就是最小的,如果 push 进来的元素比栈顶的元素还小,直接 push 进来就行,这样 minStack 栈的栈顶始终都是栈里的最小值。
{
class MinStack {
constructor() {
this.dataStack = new Stack(); // 普通的栈
this.minStack = new Stack(); // 存储最小值的栈
}
// push 和 pop 两个栈都要操作,保持大小统一
push(item) {
this.dataStack.push(item); // 常规操作
if (this.minStack.isEmpty() || item < this.minStack.top()) {
this.minStack.push(item); // 保证minStack栈顶是最小的值
} else {
this.minStack.push(this.minStack.top());
// 重复push最小值,保持两个栈的大小一样且顶部是最小的
}
}
pop() {
this.minStack.pop(); // 保持大小统一
return this.dataStack.pop(); // 返回真实的数字
}
min() {
return this.minStack.top(); // 返回最小的数字
}
}
const minstack = new MinStack();
minstack.push(3);
minstack.push(2);
minstack.push(6);
minstack.push(8);
console.log(minstack.min()); // 2
console.log(minstack.pop()); // 8
minstack.push(1);
console.log(minstack.min()); // 1
}
两个栈同步:为了保证可以 pop 掉最小的元素,当 dataStack pop 掉了最小的元素,如果 minStack 没有同步大小,可能最小的元素还在栈内
单栈
每次 push 两个值,先 push 新值,再 push 最小值
var MinStack = function() {
this.stack = []
};
MinStack.prototype.push = function(x) {
if(this.stack.length===0){
this.stack.push(x)
this.stack.push(x)
}else{
const min = this.getMin()
this.stack.push(x)
if(min<x) this.stack.push(min)
else this.stack.push(x)
}
};
MinStack.prototype.pop = function() {
this.stack.pop()
return this.stack.pop()
};
MinStack.prototype.top = function() {
return this.stack[this.stack.length-2]
};
MinStack.prototype.getMin = function() {
return this.stack[this.stack.length-1]
};
solution tips
逆序处理, 翻转, 都可以想想栈