tree

到目前为止，本书介绍了一些顺序数据结构，介绍的第一个非顺序数据结构是散列表。在本章，我们将要学习另一种非顺序数据结构——树，它对于存储需要快速查找的数据非常有用。

概述

树是一种分层数据的抽象模型。现实生活中最常见的树的例子是家谱，或是公司的组织架构图，如下图所示：

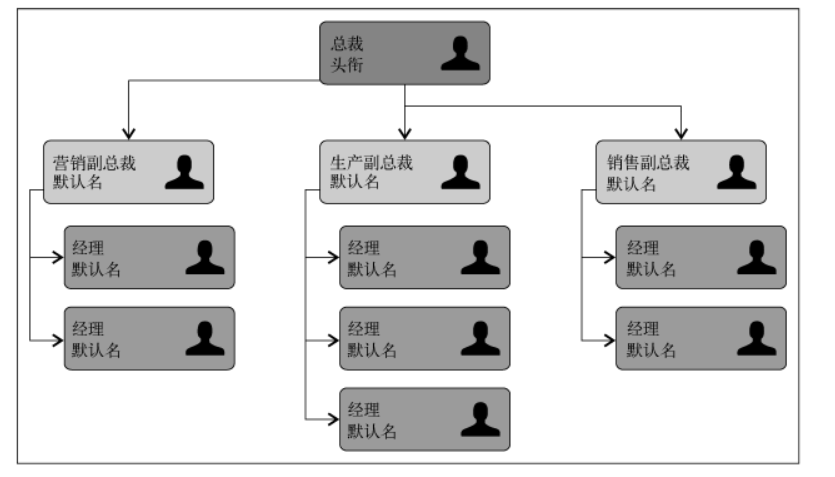
一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点（除了顶部的第一个节点）以及零个或多个子节点：

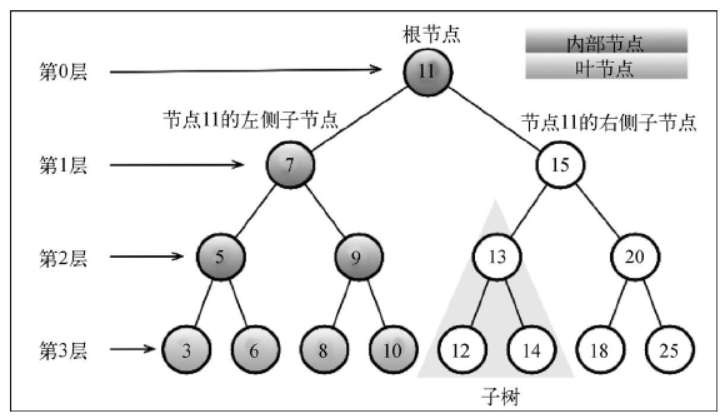
术语

位于树顶部的节点叫作根节点（11）。它没有父节点。

树中的每个元素都叫作节点，节点分为内部节点和外部节点。

至少有一个子节点的节点称为内部节点（7、5、9、15、13 和 20 是内部节点）。
没有子元素的节点称为外部节点或叶节点（3、6、8、10、12、14、18 和 25 是叶节点）。

有关树的另一个术语是子树。子树由节点和它的后代构成。例如，节点 13、12 和 14 构成了上图中树的一棵子树。子树必须包含最外部的叶子结点

节点的一个属性是深度，节点的深度取决于自身的祖先节点的数量。比如，节点 3 有 3 个祖先节点（5、7 和 11），它的深度为 3。

树的高度取决于所有节点深度的最大值。一棵树也可以被分解成层级。根节点在第 0 层，它的子节点在第 1 层，以此类推。上图中的树的高度为 3（最大高度已在图中表示——第 3 层）。

树的类型

二叉树中的节点最多只能有两个子节点：一个是左侧子节点，另一个是右侧子节点。这些定义有助于我们写出更高效的向/从树中插入、查找和删除节点的算法。二叉树在计算机科学中的应用非常广泛。

完美二叉树：每一层的子节点都是满的

完全二叉树

According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.

只有一个节点也是完全二叉树

二叉搜索树

二叉搜索树（BST）是二叉树的一种，但是它只允许你在左侧节点存储（比父节点）小的值，在右侧节点存储（比父节点）大（或者等于）的值。上一节的图中就展现了一棵二叉搜索树。

对于每一棵二叉搜索树树（子树），根节点就是这些数据的中位数 @@@

线索二叉树

Morris 遍历

BST 二叉搜索树

Binary Search Tree 类

class TreeNode { //{1}
    val = null
    key = null
    left = null
    right = null

    constructor(val) {
        this.val = val;
        this.key = val;
    }
}

class BinarySearchTree {
    root = null; //{2}
}

下图展现了二叉搜索树数据结构的组织方式：

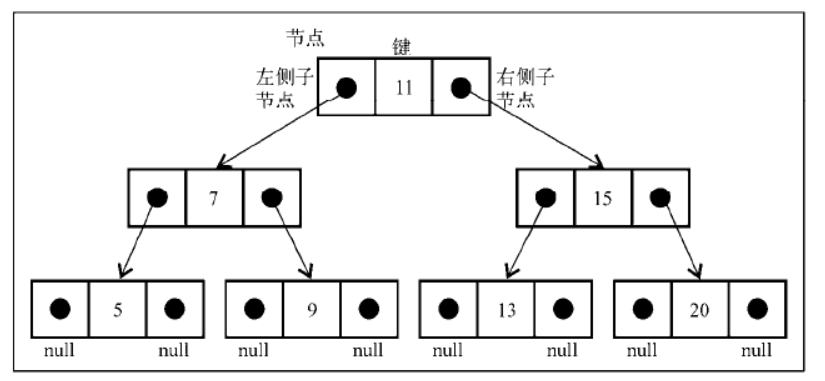
和链表一样，将通过指针来表示节点之间的关系（术语称其为边）。

在双向链表中，每个节点包含两个指针，一个指向下一个节点，另一个指向上一个节点。对于树，使用同样的方式（也使用两个指针）。但是，一个指向左侧子节点，另一个指向右侧子节点。

因此，将声明一个 Node 类来表示树中的每个节点（行{1}）。值得注意的一个小细节是，不同于在之前的章节中将节点本身称作节点或项，我们将会称其为键。键是树相关的术语中对节点的称呼。

双向链表一个节点包括：前指针数据后指针

二叉树一个节点包括：左指针键右指针

我们将会遵循和 linked-list 类中相同的模式, 这表示也将声明一个变量以控制此数据结构的第一个节点。在树中，它不再是头节点，而是根元素（行{2}）。

基本操作

insert(key)：向树中插入一个新的键。
search(key)：在树中查找一个键，如果节点存在，则返回 true；如果不存在，则返回 false。
inOrderTraverse：通过中序遍历方式遍历所有节点。
preOrderTraverse：通过先序遍历方式遍历所有节点。
postOrderTraverse：通过后序遍历方式遍历所有节点。
min：返回树中最小的值/键。
max：返回树中最大的值/键。
ceiling(key)：返回大于等于 key 的最小值，类似于 Math.ceiling(key) ，只是返回值必须是树中的键
floor(key)：返回小于等于 key 的最大值
remove(key)：从树中移除某个键。

insert()

下面的代码是用来向树插入一个新键的算法的第一部分：

    insert(key) {
        const node = new TreeNode(key);
        if (this.root === null) this.root = node;
        else this.insertNode(this.root, node);
        // 返回插入的节点
        return node;
    }

要向树中插入一个新的节点（或项），要经历三个步骤：

创建用来表示新节点的 Node 类实例。只需要向构造函数传递我们想用来插入树的节点值，它的左指针和右指针的值会由构造函数自动设置为 null。
验证这个插入操作是否为一种特殊情况。这个特殊情况就是我们要插入的节点是树的第一个节点（行{2}）。如果是，就将根节点指向新节点。
将节点加在非根节点的其他位置。这种情况下，需要一个私有的辅助函数 insertNode ，函数定义如下：

    insertNode(node, newNode) {
        if (newNode.key < node.key) {
            //{4}
            if (node.left === null) {
                //{5}
                node.left = newNode //{6}
            } else {
                this.insertNode(node.left, newNode) //{7}
            }
        } else {
            if (node.right === null) {
                //{8}
                node.right = newNode //{9}
            } else {
                this.insertNode(node.right, newNode) //{10}
            }
        }
    }

如果树非空，需要找到插入新节点的位置。因此，在调用 insertNode 方法时要通过参数传入树的根节点和要插入的节点。

正如链表必须从头部开始遍历，树必须要从根节点开始递归

如果新节点的键小于当前节点的键（初始时，当前节点就是根节点）（行{4}）那么需要检查当前节点的左侧子节点。

如果它没有左侧子节点（行{5}），就在那里插入新的节点。
如果有左侧子节点，需要通过递归调用 insertNode 方法（行{7}）继续找到树的下一层。
下次将要比较的节点将会是当前节点的左侧子节点。

如果节点的键比当前节点的键大，那么需要检查当前节点的右侧子节点。

如果当前节点没有右侧子节点（行{8}），就在那里插入新的节点（行{9}）。
如果有右侧子节点，同样需要递归调用 insertNode 方法
但是要用来和新节点比较的节点将会是右侧子节点。

示例

让我们通过一个例子来更好地理解这个过程。

首先插入第一个节点，这种情况下，树中有一个单独的节点，根指针将会指向它。源代码的行{2}将会执行。

var tree = new BinarySearchTree();

接着输入：

tree.insert(11);
tree.insert(7);
tree.insert(15);
tree.insert(5);
tree.insert(3);
tree.insert(9);
tree.insert(8);
tree.insert(10);
tree.insert(13);
tree.insert(12);
tree.insert(14);
tree.insert(20);
tree.insert(18);
tree.insert(25);

会创建如下结构：

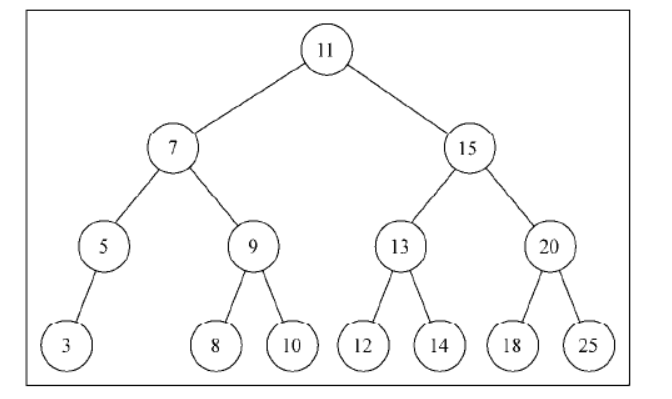
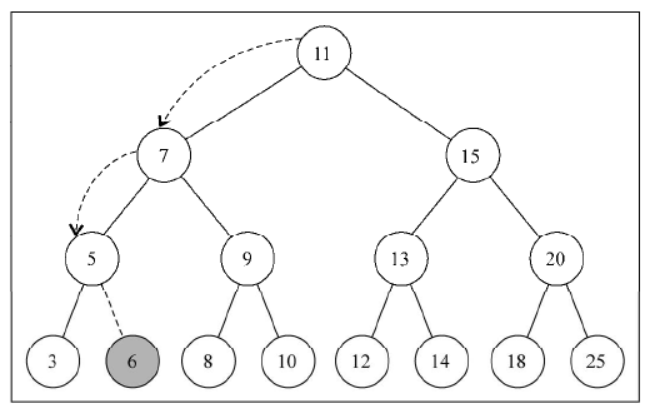
现在我们插入一个键值为 6 的节点：tree.insert(6)

树不是空的，insertNode 方法将会被调用：insertNode（root, key[6]）
算法将会检测行{4}（key[6] < root[11] 为真），并继续检测行{5}（node.left[7] 不是 null），然后将到达行{7}并调用 insertNode(node.left[7], key[6])
将再次进入 insertNode 方法内部，但是使用了不同的参数。它会再次检测行{4}（key[6] < node[7] 为真），然后再检测行{5}（node.left[5] 不是 null），接着到达行{7}，调用 insertNode（node.left[5], key[6])
将再一次进入 insertNode 方法内部。它会再次检测行{4}（key[6] < node[5] 为假），然后到达行{8}（node.right 是 null——节点 5 没有任何右侧的子节点），然后将会执行行{9}，在节点 5 的右侧子节点位置插入键 6。
然后，方法调用会依次出栈，代码执行过程结束。

search()

搜索树中的值

在树中，有三种经常执行的搜索类型：

搜索最小值
搜索最大值
搜索特定的值

搜索最小值和最大值

我们使用下面的树作为示例：

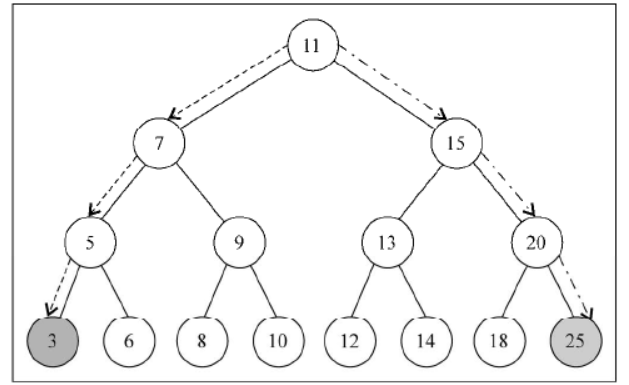
如果你看一眼树最后一层最左侧的节点，会发现它的值为 3，这是这棵树中最小的键。

如果你再看一眼树最右端的节点（同样是树的最后一层），会发现它的值为 25，这是这棵树中最大的键

这种特点在我们实现搜索树节点的最小值和最大值的方法时能给予我们很大的帮助。

搜索最小值

首先，我们来看寻找树的最小键的方法：

this.min = function () {
  return minNode(root); //{1}
};

var minNode = function (node) {
  if (node) {
    while (node && node.left !== null) {
      //{2}
      node = node.left; //{3}
    }
    // 跳出while循环，到底最底层、最左处的节点
    return node.key;
  }
  return null; //{4}
};

minNode 方法允许我们从树中任意一个节点开始寻找最小的键。我们可以使用它来找到一棵树或它的子树中最小的键。因此，我们在调用 minNode 方法的时候传入树的根节点（行{1}），因为我们想要找到整棵树的最小键。

搜索最大值

this.max = function () {
  return maxNode(root);
};

var maxNode = function (node) {
  if (node) {
    while (node && node.right !== null) {
      //{5}
      node = node.right;
    }
    return node.key;
  }
  return null;
};

要找到最大的键，我们要沿着树的右边进行遍历（行{5}）直到找到最右端的节点。

因此，对于寻找最小值，总是沿着树的左边；而对于寻找最大值，总是沿着树的右边。

搜索特定值

在之前的章节中，我们同样实现了 find、search 或 get 方法来查找数据结构中的一个特定的值（和之前章节中实现的 has 方法相似）。我们将同样在 BST 中实现搜索的方法，来看它的实现：

this.search = function (key) {
  return searchNode(root, key); //{1}
};

var searchNode = function (node, key) {
  if (node === null) {
    //{2}
    return false;
  }
  if (key < node.key) {
    //{3}
    return searchNode(node.left, key); //{4}
  } else if (key > node.key) {
    //{5}
    return searchNode(node.right, key); //{6}
  } else {
    return true; //{7}
  }
};

我们要做的第一件事，是声明 search 方法。和 BST 中声明的其他方法的模式相同，我们将会使用一个辅助函数 searchNode

searchNode 方法可以用来寻找一棵树或它的任意子树中的一个特定的值。这也是为什么在行{1}中调用它的时候传入树的根节点作为参数。

在开始算法之前，先要验证作为参数传入的 node 是否合法（不是 null）。如果是 null 的话，说明要找的键没有找到，返回 false。

如果传入的节点不是 null，需要继续验证。

如果要找的键比当前的节点小（行{3}），那么继续在左侧的子树上搜索（行{4}）
如果要找的键比当前的节点大，那么就从右侧子节点开始继续搜索（行{6}）
否则就说明要找的键和当前节点的键相等，就返回 true 来表示找到了这个键（行{7}）

700. 二叉搜索树中的搜索

ceiling(key) 和 floor(key)

ceiling(key) 函数：返回大于等于 key 的最小元素，如果不存在，返回空。

floor(key) 函数：返回小于等于 key 的最大元素，如果不存在，返回空。

floor 分析如下，在查找过程中，分 3 种情况：

key 小于当前结点的键，所以对 key 向下取整的结果肯定会在左子树，所以向左儿子递归处理
key 等于当前结点的键，也符合 floor 的定义，所以直接返回该键
key 大于当前结点的键，这种情况只能先排除左子树，在此基础上有两种可能：floor 值就是当前结点的键，或者 floor 在当前结点的右子树中，但由于条件不足无法立即给出判断，所以只能继续向右子树递归 floor 方法，并取得递归的返回值，判断递归返回的结果是否为 null
- 如果递归返回 null,说明右子树没有 floor 值，所以 floor 值就是当前结点的键，
- 如果递归不为 null,说明右子树还有比当前结点键更大的 floor 值，所以返回递归后的非 null 的 floor 值

this.floor = function (key) {
  return floorNode(root, key);
};
function floorNode(node, key) {
  if (node === null) return null;
  if (key < node.key) {
    // floor值肯定在左子树
    return floorNode(node.left, key);
  } else if (key === node.key) {
    return node.key;
  } else {
    // key>node.key
    // 有两种可能：floor值是当前结点或在右子树
    const floor = floorNode(node.right, key);
    if (floor === null) return node.key;
    else return floor;
  }
}

// ceiling
this.ceiling = function (key) {
  return ceilingNode(root, key);
};
function ceilingNode(node, key) {
  if (node === null) return false;
  if (key > node.key) {
    // ceiling值肯定在右子树
    return ceilingNode(node.right, key);
  } else if (key === node.key) {
    return node.key;
  } else {
    // key<node.key
    // 有两种可能：ceiling值是当前节点或者是左子树
    const ceiling = ceilingNode(node.left, key);
    if (ceiling === null) return node.key;
    else return ceiling;
  }
}

第 K 小的数

remove()

this.remove = function (key) {
  root = removeNode(root, key); //{1}
};

这个方法接收要移除的键并且它调用了 removeNode 方法，传入 root 和要移除的键作为参数（行{1}）。我要提醒大家的一件非常重要的事情是，root 被赋值为 removeNode 方法的返回值。我们稍后会明白其中的原因。

removeNode 方法的复杂之处在于我们要处理不同的运行场景，当然也包括它同样是通过递归来实现的。

我们来看 removeNode 方法的实现：

var deleteNode = function (root, key) {
    // 第一步找到节点, 根据 bst 的性质来递归是找的最快的
    return dfs(root, key)

    function dfs(node, key) {
        if (node === null) return node;

        if (node.val === key) {
            // 执行删除逻辑
            if (node.left === null && node.right === null) {
                // 要删除的节点是叶子节点, 直接删除就好了
                return null;
            }
            else if (node.left === null || node.right === null) {
                // 要删除的节点仅有一个子节点, 直接拼接子节点就行, 依然符合 bst
                return node.left || node.right
            }
            else {
                // 要删除的节点有两个子节点, 要找到右子树中最小的那个节点, 才能维持 bst
                let cur = node.right;
                while (cur.left !== null) {
                    prev = cur;
                    cur = cur.left;
                }

                // 删除当前 node, 值替换
                node.val = cur.val;
                // 删除替换的 node, 引用删除
                node.right = dfs(node.right, cur.val)
                return node;
            }
        }
        else if (key < node.val){
            node.left = dfs(node.left, key);
        }
        else {
            node.right = dfs(node.right, key);
        }

        return node;
    }
};

如果我们找到了要找的键（键和 node.key 相等），就需要处理三种不同的情况。

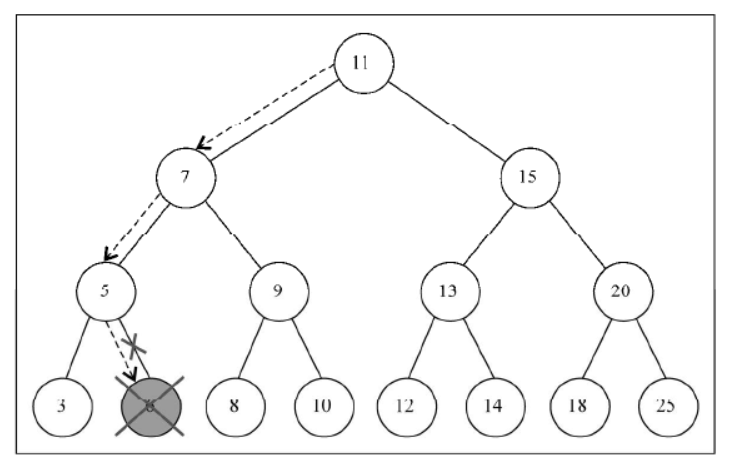
移除一个叶节点

第一种情况是该节点是一个没有左侧或右侧子节点的叶节点——行。在这种情况下，我们要做的就是给这个节点赋予 null 值来移除它。但是当学习了链表的实现之后，我们知道仅仅赋一个 null 值是不够的，还需要处理指针。在这里，这个节点没有任何子节点，但是它有一个父节点，需要通过返回 null 来将对应的父节点指针赋予 null 值

现在节点的值已经是 null 了，父节点指向它的指针也会接收到这个值，这也是我们要在函数中返回节点的值的原因。父节点总是会接收到函数的返回值。另一种可行的办法是将父节点和节点本身都作为参数传入方法内部

下图展现了移除一个叶节点的过程

移除有一个左侧或右侧子节点的节点

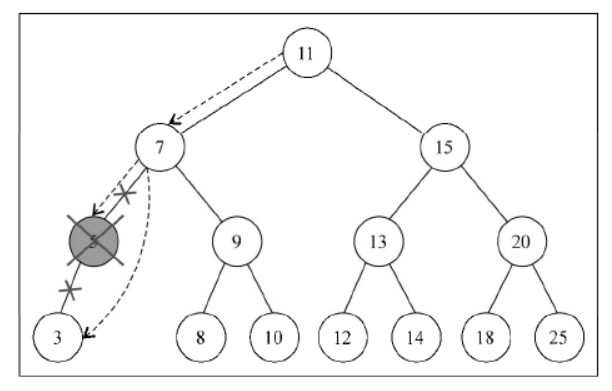
现在我们来看第二种情况，移除有一个左侧子节点或右侧子节点的节点。这种情况下，需要跳过这个节点，直接将父节点指向它的指针指向子节点

如果这个节点没有左侧子节点（行{12}），也就是说它有一个右侧子节点。那我们把父节点对它的引用改为对它右侧子节点的引用（行{13}）通过返回更新后的节点（行{14}）

如果这个节点没有右侧子节点，也是一样——把父节点对它的引用改为对它左侧子节点的引用（行{16}）通过返回更新后的值（行{17}）

下图展现了移除只有一个左侧子节点或右侧子节点的节点的过程：

移除有两个子节点的节点

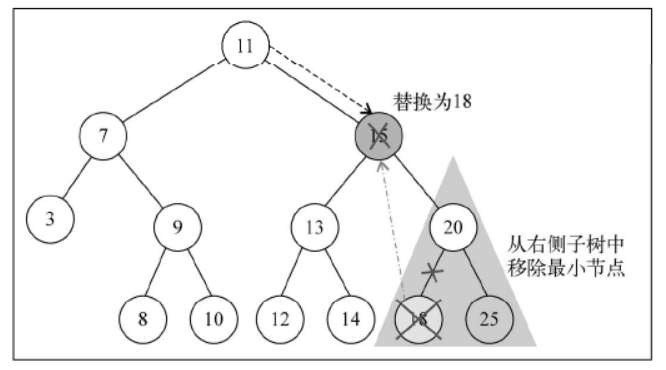
现在是第三种情况，也是最复杂的情况，那就是要移除的节点有两个子节点——左侧子节点和右侧子节点。要移除有两个子节点的节点，需要执行四个步骤。

当找到了需要移除的节点后，需要找到它右边子树中最小的节点（它的继承者——行{18}）。
然后，用它右侧子树中最小节点的键去更新这个节点的值（行{19}）。通过这一步，我们改变了这个节点的键，也就是说它被移除了。
但是，这样在树中就有两个拥有相同键的节点了，这是不行的。要继续把右侧子树中的最小节点移除，毕竟它已经被移至要移除的节点的位置了（行{20}）。
最后，向它的父节点返回更新后节点的引用（行{21}）。

findMinNode 方法的实现和 min 方法的实现方式是一样的。唯一不同之处在于，在 min 方法中只返回键，而在 findMinNode 中返回了节点。

下图展现了移除有两个子节点的节点的过程：

AVL 自平衡树

BST 存在一个问题：取决于你添加的节点数，树的一条边可能会非常深；也就是说，树的一条分支会有很多层，而其他的分支却只有几层。

这会在需要在某条边上添加、移除和搜索某个节点时引起一些性能问题。

在上面这棵二叉搜索树上查找一个元素需要花费线性时间复杂度，这跟在链表中搜索的速度是一样的。越是有序的数组这个问题越严重，现在我们来比较一下下面这棵平衡二叉搜索树。

假设这棵树上节点总数为 n，一个平衡树能把高度维持在 h=logn。因此这棵树上支持在 O(h)=O(logn) 时间内完成插入，搜索，删除操作。

为了解决这个问题，有一种树叫作 Adelson-Velskii-Landi 树（AVL 树）。AVL 树是一种自平衡二叉搜索树，意思是任何一个节点左右两侧子树的高度之差最多为 1。也就是说这种树会在添加或移除节点时尽量试着成为一棵完全树。

AVL 树是一种自平衡树。添加或移除节点时，AVL 树会尝试自平衡。任意一个节点（不论深度）的左子树和右子树高度最多相差 1。添加或移除节点时，AVL 树会尽可能尝试转换为完全树。

在 AVL 树插入节点

在 AVL 树中插入或移除节点和 BST 完全相同。然而，AVL 树的不同之处在于我们需要检验它的平衡因子，如果有需要，则将其逻辑应用于树的自平衡。

var insertNode = function (node, element) {
  if (node === null) {
    node = new Node(element);
  } else if (element < node.key) {
    node.left = insertNode(node.left, element);

    if (node.left !== null) {
      // 确认是否需要平衡 {1}
    }
  } else if (element > node.key) {
    node.right = insertNode(node.right, element);

    if (node.right !== null) {
      // 确认是否需要平衡 {2}
    }
  }
  return node;
};

计算平衡因子

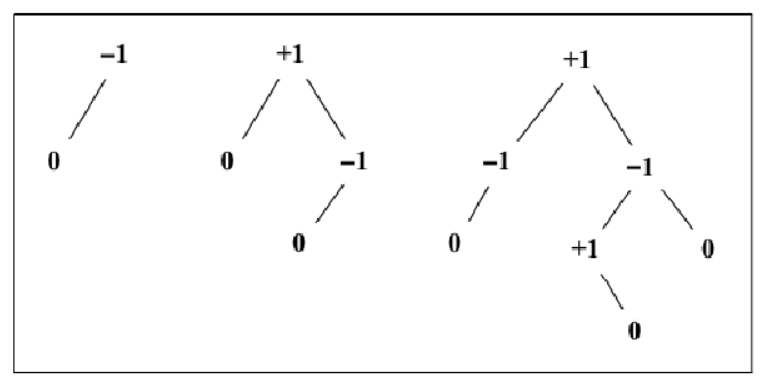
在 AVL 树中，需要对每个节点计算右子树高度（hr）和左子树高度（hl）的差值，该值（hr－hl）应为 0、1 或 -1。如果结果不是这三个值之一，则需要平衡该 AVL 树。这就是平衡因子的概念

注意：每个节点的平衡因子与子节点的平衡因子无关

下图举例说明了一些树的平衡因子（所有的树都是平衡的）：

计算节点高度的代码如下：

var heightNode = function (node) {
  if (node === null) {
    return -1;
  } else {
    return Math.max(heightNode(node.left), heightNode(node.right)) + 1;
  }
};

平衡因子：右节点高度 - 左节点高度，而不是右平衡因子 - 左平衡因子

因此，向左子树插入新节点时，需要计算其高度；如果高度差大于 1（即不为 -1、0 和 1 之一），就需要平衡左子树。代码如下：

// 替换insertNode方法的行{1}
if (heightNode(node.left) - heightNode(node.right) > 1) {
  // 旋转 {3}
}

向右子树插入新节点时，应用同样的逻辑，代码如下：

// 替换insertNode方法的行{2}
if (heightNode(node.right) - heightNode(node.left) > 1) {
  // 旋转 {4}
}

isBalanced()

var isBalanced = function (root) {
    return dfs(root) >= 0
    
    function dfs(node) {
        if (node === null) return 0;

        const leftHigh = dfs(node.left);
        const rightHigh = dfs(node.right);

        if (leftHigh === -1
            || rightHigh === -1
            || Math.abs(rightHigh - leftHigh) > 1
        ) {
            return -1;
        }

        return Math.max(leftHigh, rightHigh) + 1
    }
};

AVL 旋转

向 AVL 树插入节点时，可以执行单旋转或双旋转两种平衡操作，分别对应四种场景。

右右（RR）：向左的单旋转

左左（LL）：向右的单旋转

左右（LR）：向右的双旋转

右左（RL）：向左的双旋转

右右（RR）：向左的单旋转

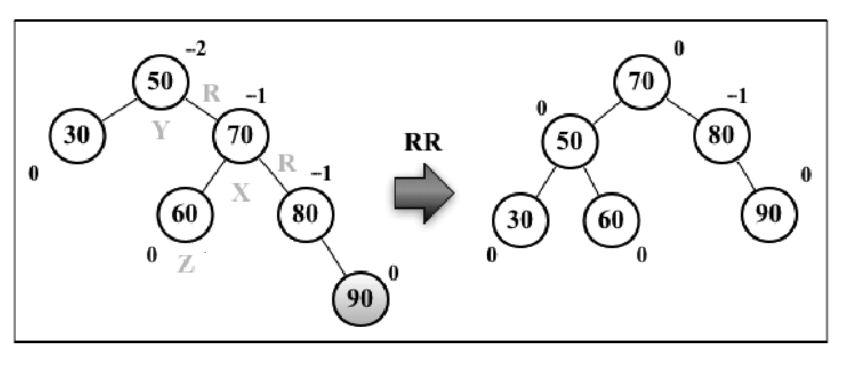
假设向 AVL 树插入节点 90，这会造成树失衡（节点 50-Y 高度为 -2），因此需要恢复树的平衡。因为是右节点的右节点导致的失衡，所以称之为 RR，所执行的操作是左旋转

与平衡操作相关的节点有三个（X、Y、Z）

操作的主要目标是节点 Y：

对节点 Y 绕着 X 进行左旋转

Y 旋转到 X 的左子树上

Z 被 Y 霸占了自己原本的位置，所以需要重新插入
Z 比 X 小，比 Y 大，应该插入到 Y 的右子树

function rotationRR(node) {
  const temp = node.right; // {1} temp = X , 保存X
  node.right = temp.left; // {2} Y.right = Z , 断开X与Y，同时修正Z的位置
  temp.left = node; // {3} X.left = Y , 修正Y的位置
  return temp;
}

左左（LL）：向右的单旋转

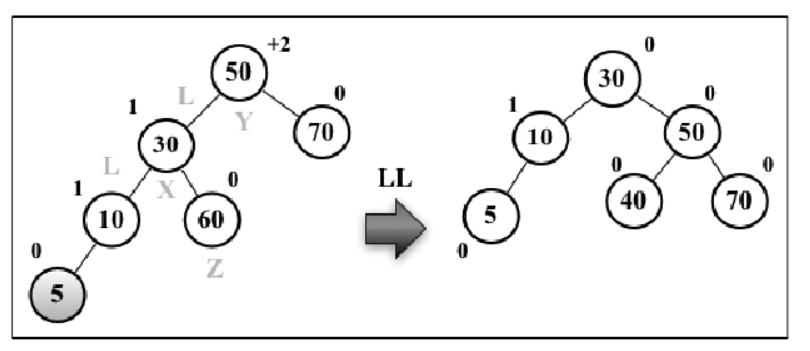
假设向 AVL 树插入节点 5，这会造成树失衡（节点 50-Y 平衡因子为 +2），需要恢复树的平衡。因为是左节点的左节点导致的失衡，所以称之为 LL，所执行的操作是右旋转

与平衡操作相关的节点有三个（X、Y、Z）

操作的主要目标是节点 Y：

对节点 Y 绕着 X 进行右旋转
Y 旋转到 X 的右子树上
Z 被 Y 霸占了自己原本的位置，所以需要重新插入
Z 比 X 大，比 Y 小，应该插入到 Y 的左子树

function rotationLL(node) {
  var tmp = node.left; // {1} temp = X , 保存X
  node.left = tmp.right; // {2} Y.left = Z , 断开X与Y，同时修正Z的位置
  tmp.right = node; // {3} X.right = Y , 修正Y的位置
  return tmp;
}

左右（LR）：先左旋转再右旋转

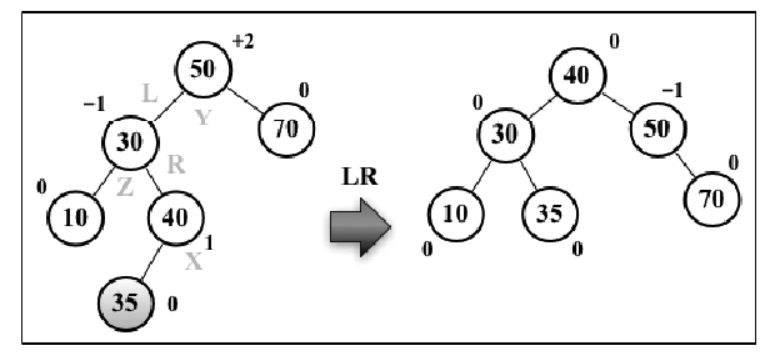
假设向 AVL 树插入节点 35，这会造成树失衡（节点 50-Y 平衡因子为 +2），需要恢复树的平衡。因为是左节点的右节点导致的失衡，所以称之为 LR，所执行的操作是先左旋转再右旋转

把先把目光聚焦在 Z 和 X：

对节点 Z 绕着 X 进行左旋转
Z 旋转到 X 的左子树上
被 Y 霸占的子节点 35，所以需要重新插入
子节点 35 比 X 小，比 Y 大，应该插入到 Y 的右子树

以上的步骤就是一次 RR 旋转，旋转完之后是这样的

此时把目光聚焦在 Y 和 X：

对节点 Y 绕着节点 X 进行右旋转
Y 被旋转到 X 的右子树上

如果 X 存在右节点，对该节点重新插入即可

以上步骤就是一个 LL 旋转，这样一个 LR 二叉树就被平衡了

function rotationLR(node) {
  node.left = rotationRR(node.left);
  return rotationLL(node);
}

右左（RL）：向左的双旋转

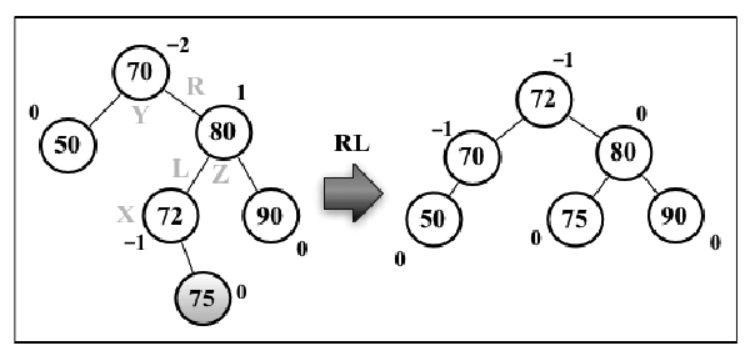
设向 AVL 树插入节点 75，这会造成树失衡（节点 70 Y 高度为 -2），需要恢复树的平衡。因为是右节点的左节点导致的失衡，所以称之为 RL，所执行的操作是先右旋转再左旋转

基本上，就是先做一次 LL 旋转，再做一次 RR 旋转。

function rotationRL(node) {
  node.right = rotationLL(node.right);
  return rotationRR(node);
}

辨别类型

出现不平衡的那个节点开始查看，那个节点就是节点 Y

然后往不平衡的方向走，走两步就决定错误的类型

完成 insertNode 方法

在实际使用中，我们总是使用自平衡二叉树，所以需要对之前实现的 insertNode 方法进行替换

向左子树插入新节点，且节点的值小于其左子节点时，应进行 LL 旋转。否则，进行 LR 旋转。该过程的代码如下：

// 替换insertNode方法的行{1}
if (heightNode(node.left) - heightNode(node.right) > 1) {
  // 旋转 {3}
  if (element < node.left.key) {
    node = rotationLL(node);
  } else {
    node = rotationLR(node);
  }
}

向右子树插入新节点，且节点的值大于其右子节点时，应进行 RR 旋转。否则，进行 RL 旋转。该过程的代码如下：

// 替换insertNode方法的行{2}
if (heightNode(node.right) - heightNode(node.left) > 1) {
  // 旋转 {4}
  if (element > node.right.key) {
    node = rotationRR(node);
  } else {
    node = rotationRL(node);
  }
}

完整代码

this.insert = function (key) {
  const newNode = new Node(key); //{1}
  if (root === null) {
    //{2}
    root = newNode;
  } else {
    // 接受顶层的变化
    root = insertNode(root, newNode); //{3}
  }
};
function insertNode(node, newNode) {
  if (node === null) {
    node = newNode;
    return node;
  }
  if (newNode.key < node.key) {
    //{4}
    node.left = insertNode(node.left, newNode); //{7}
    // 确认是否需要平衡 {1}
    if (heightNode(node.left) - heightNode(node.right) > 1) {
      // 传入需要平衡的节点
      if (newNode.key < node.left.key) node = rotationLL(node);
      else node = rotationLR(node);
    }
  } else {
    node.right = insertNode(node.right, newNode); //{10}
    // 确认是否需要平衡 {2}
    if (heightNode(node.right) - heightNode(node.left) > 1) {
      // 传入需要平衡的节点
      if (newNode.key > node.right.key) node = rotationRR(node);
      else node = rotationRL(node);
    }
  }
  // 需要返回平衡后的节点，所以和一开始的实现不太一样
  return node;
}
function heightNode(node) {
  if (node === null) {
    return -1;
  } else {
    return Math.max(heightNode(node.left), heightNode(node.right)) + 1;
  }
}

测试

var tree = new BinarySearchTree();
tree.insert(7);
tree.insert(15);
tree.insert(5);
tree.insert(3);
tree.insert(9);
tree.insert(8); // LL
tree.insert(10);
tree.insert(13); // RL
tree.insert(12); // LL
tree.insert(14); // RR
tree.insert(20);
tree.insert(18); // RR
tree.insert(25);
tree.insert(11);

完成 Remove 方法

中序遍历与二叉搜索树

二叉搜索树的一大特点就是

File	difficulty	etags	date-created
108. 将有序数组转换为二叉搜索树	easy	#leetcode/tree/bst #leetcode/divide-and-conquer	2023-06-11-Sun, 4:57:08 pm
109. 有序链表转换二叉搜索树	medium	#leetcode/tree/bst #leetcode/divide-and-conquer #leetcode/unsolved	2023-06-11-Sun, 6:46:29 pm
230. 二叉搜索树中第K小的元素	medium	#leetcode/tree/bst #leetcode/top-k #leetcode/tree/avl	2023-06-09-Fri, 8:13:39 pm
235. 二叉搜索树的最近公共祖先	medium	#leetcode/tree/traversal/path #leetcode/tree/bst #leetcode/tree/ansector #leetcode/unsolved	2023-06-15-Thu, 11:48:03 am
449. 序列化和反序列化二叉搜索树	medium	#leetcode/tree/serialize #leetcode/unsolved #leetcode/tree/bst	2023-06-09-Fri, 3:12:46 pm
530. 二叉搜索树的最小绝对差	easy	#leetcode/tree/bst	2023-06-09-Fri, 7:33:01 pm
538. 把二叉搜索树转换为累加树	medium	#leetcode/tree/bst	2023-06-09-Fri, 7:50:18 pm
669. 修剪二叉搜索树	medium	#leetcode/tree/bst	2023-06-10-Sat, 3:59:42 pm
700. 二叉搜索树中的搜索	easy	#leetcode/tree/bst #leetcode/tree/traversal/sub-tree	2023-06-09-Fri, 5:36:56 pm
95. 不同的二叉搜索树 II	medium	#leetcode/dp/fibonaci #leetcode/tree/bst #leetcode/unsolved #leetcode/divide-and-conquer	2023-06-11-Sun, 3:37:01 pm
98. 验证二叉搜索树	medium	#leetcode/tree/bst	2023-06-10-Sat, 12:51:22 pm

Low & High 构造

108 都是这种题型, 还有好几题

就是把二叉搜索树的升序排列特点利用来分治处理

File	difficulty	etags	date-created
108. 将有序数组转换为二叉搜索树	easy	#leetcode/tree/bst #leetcode/divide-and-conquer	2023-06-11-Sun, 4:57:08 pm
109. 有序链表转换二叉搜索树	medium	#leetcode/tree/bst #leetcode/divide-and-conquer #leetcode/unsolved	2023-06-11-Sun, 6:46:29 pm
95. 不同的二叉搜索树 II	medium	#leetcode/dp/fibonaci #leetcode/tree/bst #leetcode/unsolved #leetcode/divide-and-conquer	2023-06-11-Sun, 3:37:01 pm

红黑树

尽管 AVL 树是自平衡的，其插入或移除节点的性能并不总是最好的。更好的选择是红黑树。

红黑树可以高效有序地遍历其节点（http://goo.gl/OxED8K）。本书不打算讲解红黑树，但也提供了它的源代码。

哈夫曼树

二叉树变换

同样是分治的思想

File	difficulty	etags	date-created
106. 从中序与后序遍历序列构造二叉树	medium	#leetcode/tree/traversal/sub-tree #leetcode/divide-and-conquer #leetcode/unsolved	2023-06-13-Tue, 10:14:12 am
105. 从前序与中序遍历序列构造二叉树	medium	#leetcode/tree/traversal/sub-tree #leetcode/divide-and-conquer #leetcode/unsolved	2023-06-12-Mon, 2:25:56 pm

236. 二叉树的最近公共祖先

递归

复杂度分析

时间复杂度：O(N)，N 是二叉树中的节点数，最坏情况下，我们需要访问二叉树的所有节点。
空间复杂度：O(N)，这是因为递归堆栈使用的最大空间位 N,斜二叉树的高度可以是 N。

字典树

字典树，也叫“前缀树”，是一种树形结构，在解决字符串相关问题中非常高效。其提供非常快速的检索功能，常用于搜索字典中的单词，为搜索引擎提供自动搜索建议，甚至能用于 IP 路由选择。
下面展示了“top”“thus”和“their”这三个词是如何存储在字典树中的：
这些单词以从上到下的方式存储，其中绿色节点“p”，“s”和“r”分别表示“top”，“thus”和“their”的末尾

常见的字典树面试问题：

计算字典树中的总字数
打印存储在字典树中的所有单词
使用字典树对数组的元素进行排序
使用字典树从字典中形成单词
构建一个 T9 字典