!brainteasers

降维

从特殊到一般

从复杂到简单

将复杂问题看作多个子问题, 逐一解决

将复杂问题简化, 成为更熟悉的问题

直接降维

矩阵降维成数组

很直观的从一维到二维的过度, 最常见的就是矩阵的题目降维成数组的题目. 比如:

304. 二维区域和检索 - 矩阵不可变转化成多个 303. 区域和检索 - 数组不可变

反向思维

反向思维其实也是一种降维的思想, 通过取反将复杂情况降维成简单情况

补集

除了自身以外的, 等价于前缀加上后缀, 比如:

238. 除自身以外数组的乘积

从头部取加上从尾部取, 等价于取中间的, 比如:

分类讨论 / 分治法

分类讨论也是一种降维的思想, 将复杂的情况分类成多个简单情况的组合, 比如:

哨兵节点

duumyHead、动态规划初始化、等等简化理解成本的操作

sortable 哨兵

三神问题

三门问题

选必三思维与逻辑

选必三思维与逻辑_百度搜索

https://www.bilibili.com/video/BV17c411t7op/?spm_id_from=333.1007.tianma.1-1-1.click&vd_source=f8573a6196003ad3683f1c1a403d3431

十日终焉

上帝悖论的解释

时间 1: 上帝创建了一个自己举不起来的石头

时间 2: 因为上帝无所不能, 所以他强化了自身, 变得可以举起这个石头

帕斯卡的赌注

zhuanlan.zhihu.com/p/409597405

第一性原理

商业思维

全世界最大骗局其实就是鱼塘，它根本不靠钓鱼、卖鱼赚钱，他的吸金模式颠覆你的认知！

广东有个老板开了五个鱼塘，每个鱼塘都有独特的经营模式，最后一个最为赚钱。

第一个鱼塘开业，钓鱼者去钓鱼需要交 99 块钱，钓不到则免费送一只土鸡作为补偿。此消息一出，众人纷至沓来，结果每人都带着一只鸡回家。原来这位老板不是真正的养鱼人，而是专业卖鸡的，鱼塘里根本没有鱼，这就叫做去库存模式。

第二个鱼塘开业后，钓鱼不用一分钱，但钓到的鱼需以 15 元一斤的价格购买，结果前来钓鱼的人每天都能钓到数十条鱼，大家都自认是钓鱼高手，于是越来越多的人来这里享受钓鱼的乐趣。然而，这些鱼其实是老板从批发市场低价买的，再把那个鱼饿上几天，自然它就好钓了，这就叫变相营销。

第三个鱼塘开业时，老板结合了前两种模式，钓鱼不用一分钱，钓上来的鱼也可以免费拿走，但前提是必须在指定餐厅就餐，许多人高高兴兴的去钓鱼，开开心心吃烤鱼这就叫捆绑式销售。

第四个鱼塘开业只能用撒网捕鱼的方式，顾客可以扮成渔夫，穿着斗篷划船，还有专人帮忙拍照，只要钓到鱼，就可以 10 元一斤的价格购买，顾客一网下去起码都有几十斤，鱼的销量也从原来的 500 斤飙升到 5000 斤。顾客不仅能体验到捕鱼的乐趣，还能帮助批发市场解决库存问题，这就叫做杠杆效应。

第五个鱼塘开业后，老板推出了一年 298 元的会员卡，会员可以在此免费钓鱼，并提供钓鱼用品、凳子和桌子，此外还可以在这里喝茶吃饭享受 8 折优惠，这就叫做产业链服务。

色盲悖论

假设：有一个人，他有一种奇怪的色盲症。他看到的两种颜色和别人不一样，他把蓝色看成绿色，把绿色看成蓝色。

但是他自己并不知道他跟别人不一样，别人看到的天空是蓝色的，他看到的是绿色的，但是他和别人的叫法都一样，都是“蓝色”；小草是绿色的，他看到的却是蓝色的，但是他把蓝色叫做“绿色”。所以，他自己和别人都不知道他和别人的不同。

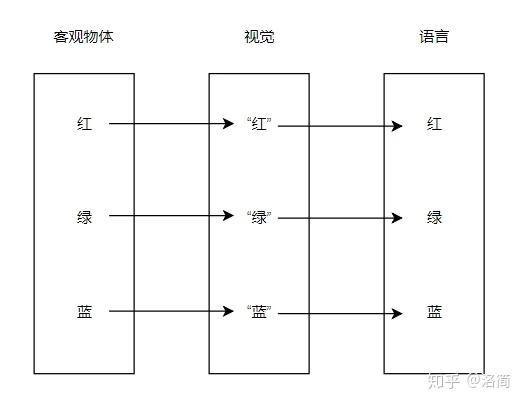
神经科学的角度：色盲和色觉差通常是由视觉系统中色感受器的不同敏感度或数量引起的。这种假设中，这个人的视觉系统处理颜色的方式与大多数人不同。

因为导致这个悖论是生理 + 语言原因

理发师悖论

通俗地理解罗素悖论，可以用理发师悖论来解释：

理发师悖论：假设在一个城市里有一个理发师，他宣称：“我只给那些不自己刮脸的人刮脸。”那么，理发师应该不应该给自己刮脸？
- 如果理发师给自己刮脸，那么他就不符合“只给那些不自己刮脸的人刮脸”的规定，因此他不应该给自己刮脸。
- 如果理发师不给自己刮脸，那么他就符合“不给自己刮脸的人”的规定，因此他应该给自己刮脸。

无论理发师是否给自己刮脸，都会引发矛盾。这种悖论揭示了某些集合（或在理发师悖论中某些规则）定义上的内在问题。

罗素悖论对集合论有深远的影响，促使数学家们重新审视集合的定义和公理体系，最终发展出更为严格和一致的集合论，如策梅洛 - 弗兰克尔集合论（Zermelo-Fraenkel set theory，ZF）以及加入选择公理的 ZF 集合论（ZFC）。

理发师悖论以及罗素悖论确实揭示了在某些集合或定义中存在的内在矛盾。这类悖论在数学和逻辑中促使了对基本概念的重新审视和调整。解决理发师悖论及其数学对应的罗素悖论，通常有以下几种方法：

类型论（Type Theory）：
- 类型论通过将对象分层次来避免自包含问题。也就是说，对象被分配到不同的类型中，每个类型只能包含低于它类型的对象。例如，集合不能包含自身，因为它们属于不同的类型。这避免了在集合内进行自引用的可能性。
策梅洛 - 弗兰克尔集合论（Zermelo-Fraenkel Set Theory, ZF）：
- ZF 集合论通过公理化集合论来避免悖论。具体地，ZF 集合论采用了“基础公理”（Axiom of Foundation），该公理禁止集合成为其自身的成员。这从根本上杜绝了类似罗素悖论的情况出现。
限制集合的定义：
- 通过严格定义什么样的集合是允许的，避免自包含的集合。例如，设定不能定义所有不包含自身的集合，这样就不会形成悖论。

具体方法说明

1. 类型论

类型论提出一种分层系统，在其中不同层次的对象不能相互引用。例如，假设有类型 0、类型 1、类型 2 等：

类型 0 可以包含基本对象（如数字）。
类型 1 可以包含类型 0 的对象和类型 0 的集合。
类型 2 可以包含类型 1 的对象和类型 1 的集合。

在这个系统中，不允许类型 1 的集合包含自身，因为它们只能包含低于或等于类型 0 的对象。

2. 策梅洛 - 弗兰克尔集合论（ZF）

ZF 集合论中有一条重要的公理——基础公理，它声明每个非空集合 A 都包含一个元素 B，使得 A 和 B 是互不相交的集合。这意味着没有集合可以包含自身，因为这种包含关系会违反基础公理。

此外，ZF 集合论通过其他公理（如分离公理和替代公理）来保证定义的集合是严格且一致的，不会产生像罗素悖论这样的自相矛盾。

3. 限制集合的定义

通过限制如何定义集合，尤其是避免定义包含自身的集合，可以从根本上防止悖论的产生。具体地，可以明确规定某些集合的定义是非法的。例如，不能定义所有不包含自身的集合。

现实中的应用

虽然理发师悖论看似是一个简单的逻辑游戏，但它确实反映了在处理集合和定义时需要注意的问题。通过采取以上的方法，可以确保定义是严谨且一致的，避免自相矛盾的情况发生。

这些方法不仅在理论上有重要意义，而且在实际应用中也提供了可靠的基础。例如，在编程语言设计、数据库理论和知识表示中，避免自引用和确保一致性是至关重要的。通过应用类型论或公理化集合论，可以构建更为稳定和可靠的系统。

阿基里斯悖论

让乌龟在阿基里斯前面 1000 米处开始，和阿基里斯赛跑，并且假定阿基里斯的速度是乌龟的 10 倍。当比赛开始后，若阿基里斯跑了 1000 米，设所用的时间为 t，此时乌龟便领先他 100 米；当阿基里斯跑完下一个 100 米时，他所用的时间为 t/10，乌龟仍然前于他 10 米；当阿基里斯跑完下一个 10 米时，他所用的时间为 t/100，乌龟仍然前于他 1 米…… 芝诺认为，阿基里斯能够继续逼近乌龟，但决不可能追上它。

阿基里斯悖论是古希腊哲学家芝诺提出的一系列关于运动和无限的悖论之一。这个悖论试图通过无限分割时间和空间来论证运动的本质问题。具体来说，它认为阿基里斯永远无法追上乌龟，即使阿基里斯的速度远远快于乌龟，因为每次阿基里斯到达乌龟之前的位置，乌龟已经移动到新的位置。

当然可以，以下是使用 LaTeX 描述的数学公式和解决方法：

阿基里斯悖论的数学解释

当然可以，以下是使用 LaTeX 描述的数学公式和解决方法：

阿基里斯悖论的数学解释

假设：

阿基里斯的速度是 ( v_A )。
乌龟的速度是 ( v_T )（其中 ( v_A = 10v_T )）。
乌龟起初领先 ( d = 1000 ) 米。

当阿基里斯跑了 ( d ) 米时，他所用的时间 ( t ) 为：

t = \frac{d}{v_{A}}

在这段时间 ( t ) 内，乌龟跑了：

d_{T} = v_{T} \times t = v_{T} \times \frac{d}{v_{A}} = \frac{d}{10} = 100 米

此时乌龟领先阿基里斯 100 米。接着阿基里斯需要跑 100 米来达到乌龟的位置，这段时间为：

t_{2} = \frac{100}{v_{A}}

在这段时间 ( t_2 ) 内，乌龟又跑了：

d_{T 2} = v_{T} \times t_{2} = v_{T} \times \frac{100}{v_{A}} = \frac{100}{10} = 10 米

同样地，每次阿基里斯到达乌龟之前的位置，乌龟总是会再跑一小段距离。

解决悖论：无限级数

为了解决这个悖论，我们需要认识到尽管有无限多个步骤，时间总和是有限的。这涉及到无限级数的求和。我们来看一下总时间 ( T )：

T = t + t_{2} + t_{3} + \dots

根据之前的计算，每个时间段是前一个的 ( \frac{1}{10} )，因此这个级数是一个等比级数：

T = t (1 + \frac{1}{10} + {(\frac{1}{10})}^{2} + {(\frac{1}{10})}^{3} + \dots)

这个等比级数的和可以用公式来求解：

S = \frac{a}{1 - r}

其中 ( a = t ) 是首项， ( r = \frac{1}{10} ) 是公比。于是我们得到：

T = \frac{t}{1 - \frac{1}{10}} = \frac{t}{0.9} = \frac{t}{\frac{9}{10}} = \frac{10}{9} t

可以看出，总时间 ( T ) 是有限的。即：

T = \frac{10}{9} t

因此，尽管阿基里斯必须通过无数个阶段才能追上乌龟，但所需的总时间是有限的，阿基里斯实际上可以在有限时间内追上并超越乌龟。

总结

芝诺的悖论通过无限分割时间和空间揭示了当时对无限概念的困惑。然而，通过现代数学，特别是对等比级数和无限求和的理解，我们可以清楚地看到尽管存在无穷多个阶段，总时间仍然是有限的，因此阿基里斯确实能够追上并超过乌龟。这个悖论在历史上对数学和哲学的研究产生了深远的影响，推动了对无限和连续性的理解。

上帝悖论

这个悖论通常被称为“上帝搬不动的石头悖论”，旨在探讨上帝的无限能力是否可能存在逻辑矛盾。让我们来分析一下这个悖论的核心：

提问：能否创造出一块上帝自己搬不动的石头？
分析可能的回答：
- 如果回答是“能”，那么上帝创造了一块他自己搬不动的石头，表明上帝在力量方面有所限制，因为他无法搬动他自己创造的这块石头。
- 如果回答是“不能”，那么上帝无法创造出一块他搬不动的石头，这意味着上帝在创造力方面有所限制，因为他不能创造这样一块石头。
推论：无论教廷如何回答，都导致上帝在某方面不是“万能的”。

解决方法和讨论

这个悖论的关键在于对上帝的“万能”这一属性的定义。传统上，上帝的“万能”被理解为能够做任何符合逻辑的事情。然而，这个悖论提出了一个看似合理但却潜在矛盾的情况。

哲学讨论：在哲学上，有几种解决这个悖论的尝试。一种解决方案是重新思考“万能”概念，将其定义为能够做所有符合逻辑的事情，而不包括无意义或自相矛盾的事情，比如创造一块自己搬不动的石头。
宗教解释：在宗教语境中，信仰上帝的“万能”可能超出了纯逻辑推理的范畴，被视为上帝能够实现神圣计划的能力，而非被动地受制于逻辑悖论。
语言游戏理论：一些哲学家倾向于认为这种悖论源于语言使用和概念定义上的限制，而非真正反映现实中上帝的属性。

总之，这个悖论引发了对上帝“万能”属性的深入思考和讨论，涉及到哲学、宗教和逻辑推理等多个领域。无论如何，这类悖论都提醒我们，在探讨抽象概念时，需要谨慎考虑语言和逻辑的限制。

FAQ

一直很想知道以前的一些以前的理论, 当下最潮流的观点是如何看待和反驳的

就比如共产主义和马克思理论, 从全球范围来看, 马克思理论很明显是错误的路线了.

现在政治学, 经济学是怎么看待和批判马克思理论的呢?

要么是有足够的证据支撑马克思主义确实是错误的路线
要么是时代背景的局限性, 需要等待下一波共产主义浪潮. 就像 ai 浪潮, web3 浪潮, 元宇宙浪潮一样

靠 gpt 就好了, 感觉比较符合实际.

神逻辑与逻辑谬误

嘴笨的人进来学，如何一句话反杀杠精，破解有毒逻辑，见招拆招、以杠治杠_哔哩哔哩_bilibili

弱智吧言论

谜题设计